/home/caml-shaving

AVL 트리 정-복하기

스스로 균형 잡는 친구

(First release)

2018-07-08

(Last update)

2023-10-31 23:44

태그: dev

Binary Search Tree

AVL 트리를 이해하기 위해서는 BST를 먼저 알아야 한다. BST는 다음 세 가지를 만족하는 그래프이다.

Tree: Cycle이 없다.
Binary: 자식이 최대 두개이다. 따라서 자식 노드를 left, right로 구분한다.
Search Property: 모든 서브트리에 대해서 검색 성질을 만족한다. 검색 성질이란 모든 노드에 대해서 node->left < node < node->right 의 순서(order)를 만족하는 것을 말한다.

이 세 가지 조건을 만족하는 데이터 구조를 BST라고 한다. 여기서는 문제 풀이 수준에서 써먹을 수 있는 AVL 트리를 만들어 볼 것이다.

기본 구조

BST의 기본 구조는 다음과 같다.

struct Node {
  int id;      // id
  Node *left;  // left child
  Node *right; // right child
};

Search

검색 함수는 다음과 같다.

int search(Node* root, int id){
  if (root == nullptr)
    return -1; // not found

  if(id < root->id)
    return search(root->left, id);
  else if(root->id < id)
    return search(root->right, id);
  else
    return id;
}

BST의 모든 노드가 검색 성질을 만족하기 때문에, 현재 방문한 노드를 기준으로 키 값을 비교하여 다음에 방문할 노드를 알 수 있다. 따라서 ‘균형 잡힌’ BST에서 최대 방문 횟수는 루트로부터 시작하는 longest path의 길이 (=height)가 되므로 복잡도는 O(log N)이 된다.

Insert

BST에 노드를 추가하는 작업은 검색과 비슷하다. 루트 노드에서부터 노드가 삽입될 적절한 위치를 찾는다. 만약에 이미 삽입할 노드가 존재한다면, 즉 키 값에 해당하는 노드가 이미 있으면, 알아서 적절히 처리하면 된다. 이미 있는 노드를 그냥 냅두면 집합 자료구조인 Set이 되고, 같은 키를 갖는 노드의 개수를 센다면 MultiSet과 같은 자료구조가 된다.

Node* insert(Node* node, int id){
  if(node == nullptr)
    return gen_node(id);

  if(id < node->id)
    node->left = insert(node->left, id);
  else if(node->id < id)
    node->right = insert(node->right, id);
  else
    return node;
}

이때 새로운 노드를 만든느 gen_node 함수는 적절히 만들면 된다. 직접 동적 할당으로 메모리를 잡아도 되고, 문제 풀이 같은 경우는 글로벌 메모리 풀 택틱을 이용해서 pseudo-alloc을 해줘도 된다.

Remove

BST에서 노드를 삭제하는 작업은 역시 검색/추가와 비슷하지만, 추가적으로 해야할 일이 있다. 어떤 노드를 삭제할 때, 매달려 있는 자식이 없는 경우는 그저 노드를 지우기만 하면 된다. 하지만 그렇지 않은 경우, 삭제할 노드를 다른 적절한 노드와 바꿔줘야 한다. 그래야 검색 성질을 유지할 수 있다. 이때 ‘적절한 노드’란, 검색 성질을 유지하기 위해서 순서에 맞는 다음 노드이다. 예를 들어 검색 성질이 단순히 노드 아이디 사이의 대소 비교 less(<)라면, 지울 노드의 아이디보다 큰 아이디의 노드들 중 가장 작은 아이디의 노드가 적절한 노드가 될 것이다. 따라서 다음과 같이 함수를 정의할 수 있다.

Node* remove(Node* node, int id){
  if(node == nullptr) // empty tree
    return nullptr;

  // find the node to remove
  if (id < node->id)
    node->left = remove(node->left, id);
  else if (node->id < id)
    node->right = remove(node->right, id);
  else {
    // id found
    Node* l = node->left;
    Node* r = node->right;
    if (l == nullptr || r == nullptr) {
      // zero or one child only
      node = l == nullptr ? r : l;
    } else {
      // two children
      Node* very_next = left_most(r);
      node->id = very_next->id;
      node->right = remove(r, very_next->id);
    }
  }

  // after remove, tree can be empty
  if (node == nullptr)
    return nullptr;
}

지우고자 하는 노드를 찾은 경우, 노드의 자식이 없거나, 하나이거나, 두 개인 경우를 각각 나눠서 처리한 부분만 주의하면 나머지는 trivial하다. 위의 코드는 글로벌 메모리 택틱을 사용한 경우에 삭제하는 코드이다. 그래서 두 가지 해킹이 들어갔는데, (1) 먼저 삭제할 노드의 메모리를 직접적으로 해제하지 않았고, (2) 또 삭제할 노드의 바로 다음 노드를 가져오는 게 아니라 id 값을 직접 복사하고 있음을 알 수 있다. 만약 동적 할당으로 노드를 만든 더 일반적인 구현의 경우에는 (1)과 (2) 처럼 하면 안되고 조심해서 메모리를 해제하고, 노드의 값을 복사하는게 아니라 포인터만 옮기는 것이 좋다.

이때 자식이 두 개인 경우 바로 다음 순서의 노드를 구하는 함수는 다음과 같이 정의할 수 있다.

Node* left_most(Node* node){
  Node* cur = node;
  while(cur->left != nullptr){
    cur = cur->left;
  }
  return cur;
}

즉, 오른쪽 서브트리의 가장 왼쪽 노드를 찾으면 된다. 검색 성질을 만족하기 때문에, 이 함수를 루트를 넘겨서 호출하면 가장 order가 작은 값이 되고, 반대로 right_most를 호출하면 가장 order가 큰 값이 된다

Traverse

BST는 검색 성질을 만족하기 때문에, root로부터 중위 순회를 하면 그냥 정렬된 순서가 된다.

void in_order(Node* node){
  if (node != nullptr) {
    in_order(node->left);
    visit(node);  // visit this node and do something
    in_order(node->right);
  }
}

다른 두 순회 방법인 pre-order, post-order는 visit의 순서만 달라질 뿐 기본적인 구조는 in-order와 동일하다.

Problem: Skewed Tree

BST는 강력한 자료 구조이지만, 삽입과 삭제의 순서에 따라 트리가 한쪽으로 쏠리는 (Skewed) 문제가 있다. 예를 들어, BST에 순서대로 3, 4, 2, 1, 5 가 삽입된다면, 3을 root로 하는 균형적인 트리가 생성될 것이다.

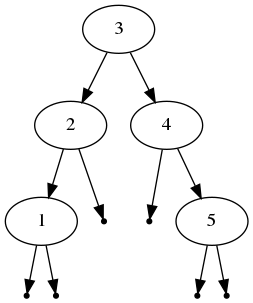
tree-1

하지만, 1, 2, 3, 4, 5 와 같이 정렬된 순서로 노드가 삽입된다면, 트리의 모양이 한쪽으로 편향되게 되고 트리의 높이가 O(N)이 되므로 O(logN)의 장점을 잃게 된다.

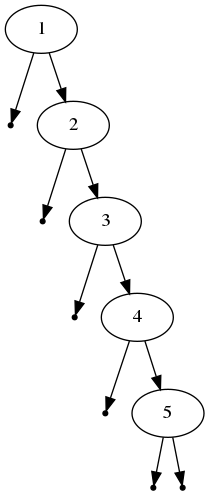
skewed

이 문제를 해결하기 위한 Self-Balanced BST 중 하나가 바로 AVL Tree이다.

AVL Tree

AVL의 뜻은 그냥 만든 사람들 이름인 Adelson-Velskii, Landis의 이니셜을 순서대로 따온 것이다.

기본적인 아이디어는 다음과 같다:

Height-Balance Property: 높이 균형 성질. 트리 내부의 모든 노드에 대하여, 노드의 자식 서브 트리의 높이의 차이가 최대 1인 성질을 말한다.
임의의 트리가 높이 균형 성질을 만족할 때, 이 트리를 AVL 트리라고 한다.

이 성질을 만족하기 위해 두 가지를 다음과 같이 정의한다:

트리의 높이: 트리의 루트 노드로부터 leaf 노드까지의 경로의 길이 중 가장 긴 것
노드의 높이: 노드로부터 leaf 노드까지의 경로의 길이 중 가장 긴 것

이때 null 노드의 길이를 -1로 정의하면, 어떤 노드의 높이는 다음과 같이 정의할 수 있다.

height(node) = max(height(node->right), height(node->left)) + 1;

AVL 트리에 노드를 삽입/삭제하는 경우, 루트로부터 해당 노드까지의 경로에 있는 노드들의 높이만 바뀌므로, 노드마다 높이를 캐싱하면 효율적인 계산이 가능하다. 따라서 기본적인 BST에서 AVL 트리로 확장하기 위해 다음과 같이 기본 구조에 높이를 추가하면 좋다.

struct Node{
  int id;
  Node* left;
  Node* right;
  int height;
};

높이를 구하는 함수는 다음과 같다.

int height(Node* node) {
  if(node == nullptr)
    return -1;
  else
    return node->height;
}

노드의 높이를 업데이트하여 캐싱하는 함수는 다음과 같다.

void update_height(Node* node) {
  node->height = max(height(node->right), height(node->left)) + 1;
}

이제 균형을 맞추기 위한 밑준비가 끝났다. 그럼 어떻게 균형을 맞출 수 있을까?

Rotation

균형이 깨진 트리를 생각해보자.

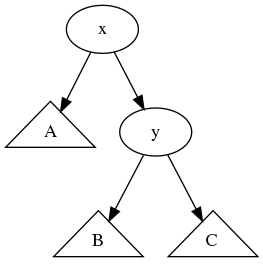
right_skewed

x의 왼쪽 서브 트리의 높이보다 오른쪽 서브 트리의 높이가 더 큰 상황이다. 편의를 위해 오른쪽 서브 트리는 서브 트리의 루트(y)를 표시했다. 또한 이때 서브 트리의 높이를 살펴보면, height(A) = k 라고 했을 때, height(y) = k+2 가 될 것이므로 height(B) 또는 height(C) 가 k+1 인 경우이다. B, C 모두 k+1이라고 하자.

이렇게 x의 오른쪽 균형이 깨진 상황에서 다시 균형을 맞추기 위한 답은 간단하다. x를 기준으로 왼쪽으로 회전하면 된다. 원래 루트인 x가 회전 후 왼쪽으로 가기 때문에 왼쪽으로 회전한다고 표현한다. 즉, 잘 회전해서 아래와 같은 트리를 만들면 된다. 이 연산은 그저 노드의 부모와 자식을 바꾸는 연산이기 때문에 O(1)만에 수행 가능하다.

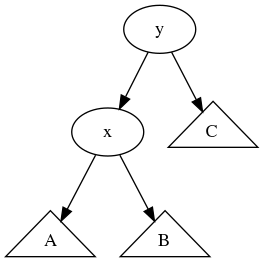
right_skewed_left_rotate

이렇게 회전을 하고 나면, x를 기준으로 height(A) = k, height(B) = k+1 이 되므로 x는 균형이 맞고, y를 기준으로는 height(x) = max(height(A), height(B)) + 1 이므로 k+2가 되고 height(C) = k+1이 되므로 모든 서브 트리가 균형이 맞게 된다.

이를 코드로 나타내면 다음과 같다.

Node* left_rotate(Node* x) {
  Node* y = x->right;
  Node* B = y->left;

  y->left = x;
  x->right = B;

  update_height(x);
  update_height(y);

  return y;
}

x를 기준으로 회전을 하고 나면 루트가 y로 바뀌기 때문에 return 할 루트 노드가 y로 변하는 것에 주의해야 한다.

왼쪽으로 균형이 치우친 경우는 앞서 설명한 경우의 mirrored image 이므로 다음과 같이 오른쪽으로 회전하는 함수를 통해 해결할 수 있다.

Node* right_rotate(Node* y) {
  Node* x = y->left;
  Node* B = x->right;

  y->left = B;
  x->right = y;

  update_height(x);
  update_height(y);

  return x;
}

역시 루트가 y에서 x로 바뀌기 때문에 return 할 노드가 달라지는 것에 주의하면 된다.

이제 양쪽 높이가 다른 경우 회전을 통해 다시 균형을 맞출 수 있게 되었다. 하지만 완벽한 균형을 맞추기 위해서는 한 가지가 더 필요하다.

Balance

균형이 오른쪽으로 치우친 경우를 좀더 생각해보자. 왼쪽으로 한번만 회전한다고 균형을 제대로 맞출 수 있을까? 아래와 같은 경우를 생각해보자.

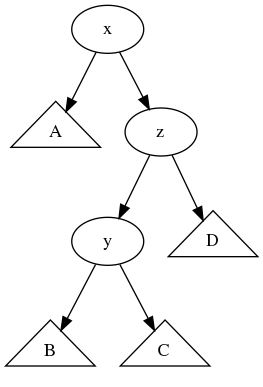
rl_skewed

이 경우는 D의 서브트리에서 노드가 삭제되는 경우 발생할 수 있다. 높이를 따져보면 height(D)=k 라고 했을 때, height(y)=k+2, height(z)=k+3, height(A)=k+1, height(x)=k+4 인 경우가 있다. 따라서 x와 z 모두 균형이 깨져있는 상태이다. x는 오른쪽 서브트리가, z는 왼쪽 서브트리가 균형이 맞지 않는다.

x를 기준으로 오른쪽으로 치우쳐있으므로 왼쪽으로 한번만 회전하면 될 것 같다. 하지만 왼쪽으로 회전하면 다음과 같이 여전히 균형이 깨진 트리가 나온다.

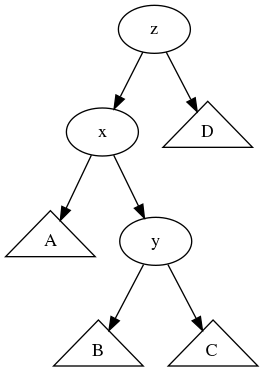
rl_skewed_wrong_rotate

정말 그럴까? 높이를 확인해보면 height(D)=k, height(y)=k+2, height(A)=k+1, height(x)=k+3, height(z)=k+4 가 되므로, 여전히 z의 균형은 깨져 있다.

이런 경우에는 어떻게 해야할까?

정답은 [두번 회전]이다. 다만 첫번째 회전을 자식의 균형을 보고 해야 한다. 처음 트리에서 x의 오른쪽 자식 노드인 z를 기준으로 양쪽 높이를 확인하여 왼쪽으로 치우쳐 있다면, z를 기준으로 오른쪽으로 한번 회전하면 아래와 같은 모양이 나온다.

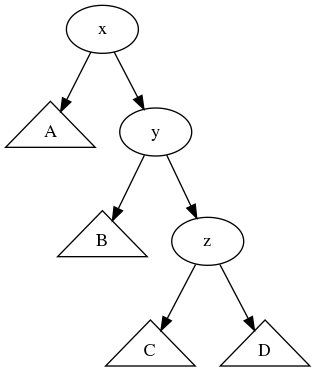
rl_skewed_rotate_z

높이를 따져보면 height(D)=k, height(C)=k+1 이므로 height(z)=k+2, height(B)=k+1 이므로 height(y)=k+3, height(A)=k+1, height(x)=k+4 가 된다. 즉 한쪽으로만 치우친(원래 루트 노드인 x만 균형이 깨진), 우리에게 익숙한 모양을 얻는다. 이상태에서 x를 기준으로 왼쪽으로 회전하면 아래와 같이 이쁘게 균형 잡힌 트리를 얻을 수 있다.

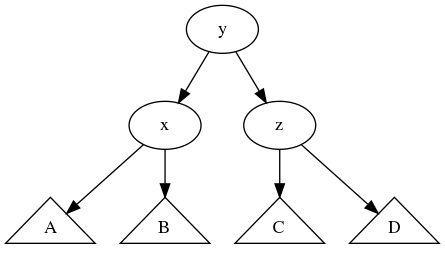
rl_skewed_rotate_x

역시 높이를 살펴보면 height(A)=k+1, height(B)=k+1 이므로 x의 균형도 맞고, height(C)=k+1, height(D)=k 이므로 z의 균형도 맞고, height(x)=k+2, height(z)=k+2 이므로 새로운 루트 노드 y의 균형도 맞는다.

반대쪽으로 치우친 경우는 이 경우의 mirrored image이므로 생략한다.

이제 준비가 끝났다. 양쪽 서브 트리의 높이 차이를 이용해서 균형이 깨진 경우를 파악하고, 추가적으로 [두번 회전] 해야 하는 경우도 파악하여 균형을 맞추는 balance 함수를 다음과 같이 정의할 수 있다.

Node* balance(Node* node) {
  static int balancing_factor = 1;
  int hl = height(node->left), hr = height(node->right);

  if (hl > hr + balancing_factor) {
    Node* l = node->left;
    int hll = height(l->left), hlr = height(l->right);
    if (hll < hlr) {
      node->left = left_rotate(node->left);
    }
    return right_rotate(node);
  }
  else if (hr > hl + balancing_factor) {
    Node* r = node->right;
    int hrl = height(r->left), hrr = height(r->right);
    if (hrl > hrr) {
      node->right = right_rotate(node->right);
    }
    return left_rotate(node);
  }
  else {
    return node;
  }
}

이때 양쪽 서브 트리의 높이의 차를 balancing_factor로 선언해두면 이 값을 적절하게 조절할 수 있다. 참고로 OCaml의 stdlib가 제공하는 Set 모듈은 balancing_factor = 2인 AVL Tree를 제공한다.

AVL Insert & Remove

이렇게 만든 balance 함수를 이용하면 AVL Tree의 삽입/삭제 함수를 다음과 같이 정의할 수 있다.

Node* insert(Node* node, int id) {
  if (node == nullptr)
    return gen_node(id);

  if (id < node->id)
    node->left = insert(node->left, id);
  else if (node->id < id)
    node->right = insert(node->right, id);
  else
    return node;

  update_height(node);

  return balance(node);
}

Node* remove(Node* node, int id) {
  if (node == nullptr)
    return nullptr;

  if (id < node->id)
    node->left = remove(node->left, id);
  else if (node->id < id)
    node->right = remove(node->right, id);
  else{
    // id found
    Node* l = node->left;
    Node* r = node->right;
    if (l == nullptr || r == nullptr) {
      node = l == nullptr ? r : l;
    } else {
      // two children
      Node* very_next = left_most(r);
      node->id = very_next->id;
      node->right = remove(r, very_next->id);
    }
  }

  if (node == nullptr)
    return nullptr;

  update_height(node);

  return balance(node);
}

이전의 BST의 삽입/삭제 로직과 거의 유사하지만, 연산이 끝난 후 (1) 높이를 새로 계산하여 업데이트해주고 (2) 이렇게 구한 높이를 이용하여 밸런싱을 해서 균형을 맞춘다.

여기까지가 AVL 트리의 야매 구현의 전부이다. AVL이라는 무시무시한 이름에 비해 생각보다 순한 내용이었다.

(번외) 디버깅 잘하기

트리와 같은 구조적 데이터는 디버깅하기 꽤 까다롭다. 배열이나 리스트의 경우 그냥 일렬로 쭉 출력해보면 뭘 잘못했는지 알기 쉬운데, 트리는 그림을 그려보지 않으면 어디가 잘못됐는지 바로 확인하기가 힘들다. pre/in/post-order로 트리를 순회하면서 출력하여 디버깅하는 방법도 있지만, 이것도 트리의 크기가 커지면 알아보기가 힘들다. 이런 구조적인 데이터 타입을 디버깅하기 위해 그래프를 그려주는 툴을 소개한다.

Graphviz

데비안 패키지에서 기본적으로 설치할 수 있는 Graphviz라는 프로그램을 쓰면 쉽게 눈으로 확인할 수 있다. sudo apt-get install graphviz로 설치할 수 있다. graphviz는 기본적으로 *.dot 파일을 입력으로 받아서 그래프를 그린다. 트리를 그리기 위해서 모든 문법을 알 필요는 없고, 방향성이 있는 digraph를 그리는 방법만 알면 된다. 문법은 매우 쉽다. DOT Language라는 언어로 작성한다.

digraph [graph name]{
  node [shape=ellipse];
  1 -> 2;
  2 -> 3;
  2 -> 4;
  null0 [shape=point];
  4 -> null0;
  null1 [shape=point];
  4 -> null1;
}

첫줄에 digraph 키워드로 해당 dot 파일이 방향성 있는 그래프를 담고 있다고 알려준다. 트리는 사이클이 없는 방향성이 있는 그래프이므로 이걸로 그릴 수 있다. 그리고 중괄호 {} 안에 노드와 엣지 정보를 그려주면 된다. 엣지 정보는 소스 노드 -> 싱크 노드로 매우 직관적인 화살표(->)를 이용해 그려주면 된다. 이게 끝이다. 이렇게 그래프의 구조를 dot 파일에 쓰고 나면 dot -Tpng -O [file-name].dot 커맨드로 해당 파일을 png 파일로 뽑아낼 수 있다. 그럼 아래와 같은 아름다운 트리 구조를 보며 눈으로 디버깅 할 수 있다.

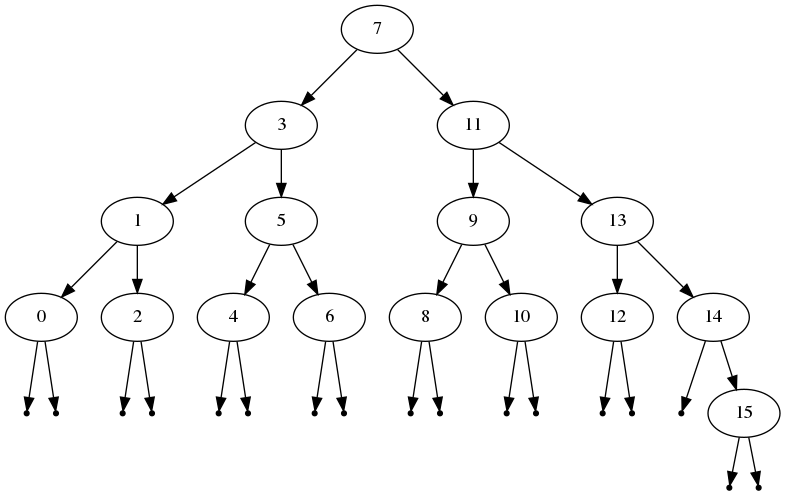
tree_example

그저 노드 정보와 엣지 정보만 알려주면 dot 파일이 최적의 형태로 그래프를 그려주기 때문에 우리는 어떤 노드가 루트이고 어떤 순서로 방문해야 하는지를 전혀 신경쓰지 않아도 된다.

Print to Dot

dot 파일을 생성하기 위한 코드는 다음과 같다.

void aux_null(int id, std::ofstream &out) {
  static int null_id = 0;
  out << "null" << null_id << " [shape=point];\n";
  out << id << " -> " << "null" << null_id << ";\n";
  ++null_id;
}

void aux_dot (Node* node, std::ofstream &out) {
  if (node->left != nullptr) {
    out << node->id << " -> " << node->left->id << ";\n";
    aux_dot(node->left, out);
  } else
    aux_null(node->id, out);

  if (node->right != nullptr) {
    out << node->id << " -> " << node->right->id << ";\n";
    aux_dot(node->right, out);
  } else
    aux_null(node->id, out);
}

void print_dot(Node* root, char* filename) {
  std::ofstream dot(filename);
  if (dot.is_open()) {
    dot << "digraph avltree{\nnode [shape=ellipse];\n";
    aux_dot(root, dot);
    dot << "}";
    dot.close();
  } else {
    printf("Unable to open file: %s\n", filename);
  }
}