Pacific Atlantic Water Flow

m x n 크기의 사각형 모양의 섬 정보가 주어진다. 섬은 태평양(Pacific Ocean)과 대서양(Atlantic Ocean) 모두에 둘러쌓여 있다. 태평양은 왼쪽과 위쪽에, 대서양은 오른쪽과 아래쪽에 있다.

섬 정보는 heights 배열로 주어지는데 heights[row][col]은 섬의 (row, col) 위치에서의 땅의 높이를 나타낸다.

섬에는 비가 엄청나게 많이 오는데, 비는 현재 땅의 동서남북으로 인접한 땅 중에서 높이가 같거나 더 작은 곳으로 흘러내린다. 최종적으로 비는 태평양과 대서양으로 흘러간다.

이때, 비가 양쪽 바다 모두로 흘러갈 수 있는 땅의 좌표의 리스트를 구하자.

\(1 \leq m, n \leq 200\) 이고 높이는 \(0 \sim 10^5\) 이다.

예를 들어 아래 땅을 보자.

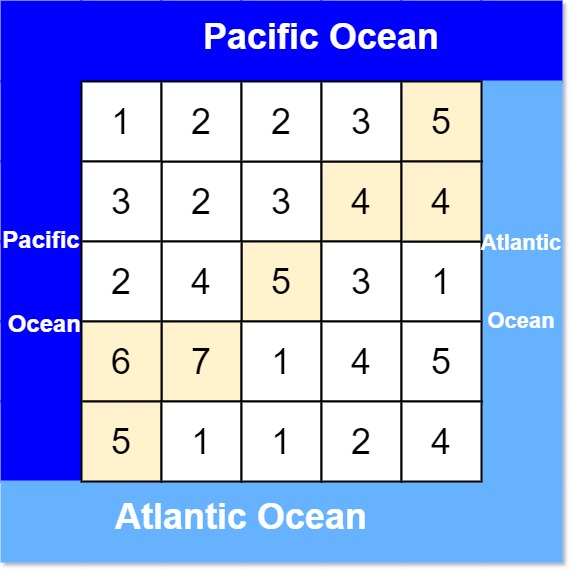
그림에서 노랗게 칠해진 땅은 비가 양 쪽 바다 모두로 흘러갈 수 있다. 따라서 답은 이 땅들의 좌표 목록이다.

그래프 탐색

이거 꽤나 신박한 그래프 탐색 문제라서 재밌게 풀었다.

일단 언뜻 생각하기에 가장 높은 곳을 찾아서 어찌 해야할 것 같지만, 잘 생각해보면 가장 높은 곳이 아니라 인접한 땅을 기준으로 가장 높은 곳을 찾아야 한다. 그런데 이렇게 찾을려면 전체 배열을 뒤지면서 각 땅마다 네 방향을 다 봐야한다. 거기다 이 높은 지점들을 찾더라도 이 지점들 중에서 양쪽 바다로 모두 흘러갈 수 있는 곳을 또 찾아야 한다. 즉, 문제의 조건을 그대로 시뮬레이션 하기에는 꽤 복잡하다.

그래서 약간 발상의 전환이 필요한데, 문제를 듀얼로 생각해보는 것이다. 그러니까 비가 흘러서 내려가는게 아니라, 거꾸로 바다에서 물이 땅을 따라 올라간다고 생각해보자. 즉 바다와 인접한 모든 땅에서 출발해서, 네 방향 중 더 높거나 같은 높이의 땅으로 타고 올라가면서 땅을 적신다고 해보자. 그러면 태평양이 적실 수 있는 땅과 대서양이 적실 수 있는 땅의 집합이 나오는데, 이 두 집합의 교집합이 결국 우리가 원하는 답이 됨을 알 수 있다.

바다가 적실 땅을 알아보려면 결국 그래프 탐색이 필요하다. 여기서는 BFS로 탐색하자. 그러면 BFS의 입력으로 탐색에 쓰일 큐를 직접 받는 게 좋아보인다. 왜냐하면 태평양과 대서양의 출발 지점이 각각 다르기 때문이다. 그걸 제외하면 탐색 알고리즘은 동일하다. 탐색 결과로는 방문한 모든 땅의 집합을 리턴하면 된다. 그래야 최종적으로 두 바다에서 모두에서 방문 가능한 땅의 위치를 알 수 있다.

from collections import deque
def pacificAtlantic(heights):
    m, n = len(heights), len(heights[0])
    def bfs(queue):
        lands = set()
        acc = [(1, 0), (0, 1), (-1, 0), (0, -1)]
        while queue:
            cur = queue.popleft()
            lands.add(cur)
            for dx, dy in acc:
                cand = (cur[0] + dx, cur[1] + dy)
                if cand[0] < 0 or cand[1] < 0 or cand[0] >= m or cand[1] >= n:
                    continue
                if cand in lands:
                    continue
                if heights[cand[0]][cand[1]] >= heights[cur[0]][cur[1]]:
                    queue.append(cand)
        return lands

    pacific, atlantic = deque(), deque()
    for c in range(n):
        pacific.append((0, c))
        atlantic.append((m - 1, c))
    for r in range(m):
        pacific.append((r, 0))
        atlantic.append((r, n - 1))
    return bfs(pacific) & bfs(atlantic)