The Most Similar Path in a Graph

n개의 도시가 있고 m개의 양방향 도로 정보 roads가 주어져서 roads[i] = (ai, bi)는 도시 ai와 도시 bi를 연결한다. 각각의 도시는 정확히 세 개의 대문자로 이뤄진 이름을 가지고 이 정보는 names로 주어진다. 어떤 도시 x에서 시작해서 x가 아닌 어떤 도시 y에도 도달할 수 있다. 즉, 도시와 도로는 무향 연결 그래프를 형성한다.

문자열 배열 targetPath가 주어진다. targetPath와 같은 길이를 가지면서 동시에 최소 수정 거리를 갖는 경로를 그래프에서 찾아야 한다.

최소 수정 거리를 갖는 경로의 노드 순서로 정답을 구해야 한다. 경로는 targetPath의 길이와 같아야 하고, 유효해야 한다 (즉, ans[i]와 ans[i+1] 사이에는 곧바로 길이 있어야 함). 정답이 여러개인 경우 아무거나 리턴해도 된다.

수정 거리는 다음과 같이 정의된다:

define editDistance(targetPath, myPath) {
    dis := 0
    a := targetPath.length
    b := myPath.length
    if a != b {
        return 10000000000000
    }
    for (i := 0; i < a; i += 1) {
        if targetPath[i] != myPath[i] {
            dis += 1
        }
    }
    return dis
}

• \[2 \leq n \leq 100\]
• m == roads.length
• \[(n-1) \leq m \leq (n \times (n-1) / 2)\]
• \[0 \leq a_i, b_i \leq n-1\]
• \[a_i != b_i\]
• 그래프는 연결 그래프임이 보장되고 각각의 노드는 최대 하나의 직통 도로를 갖는다.
• n == names.length
• names[i].length == 3
• names[i]는 대문자 알파벳만 포함한다.
• 같은 이름을 갖는 두 개의 도시가 있을 수 있다.
• \[1 \leq | targetPath | \leq 100\]
• targetPath[i].length == 3
• targetPath[i]는 대문자 알파벳만 포함한다.

예를 들어 다음과 같은 그래프를 생각해보자

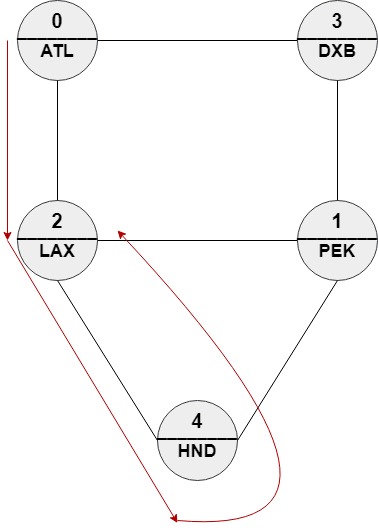
n = 5이고 roads = [(0,2), (0,3), (1,2), (1,3), (1,4), (2,4)], names = ["ATL", "PEK", "LAX", "DXB", "HND"], targetPath = ["ATL", "DXB", "HND", "LAX"]이다. 그러면 [0,2,4,2], [0,3,0,2], [0,3,1,2] 세 가지가 가능한 정답이 된다. 세 경로 모두 targetPath와 수정 거리가 1이다.