Upper Bound and Lower Bound

Mathematical Definition

Upper Bound와 Lower Bound의 수학적인 정의는 다음과 같다. 어떤 순서 있는 집합(구체적으로는 Preorder, 즉 reflexive + transitive 한 순서이고, 보통은 <= 라고 이해하면 된다)의 부분 집합 S에 대해서,

• S의 Upper Bound: S의 모든 원소보다 크거나 같은 원소 K
• S의 Lower Bound: S의 모든 원소보다 작거나 같은 원소 K

이때 각 Bound인 K는 S안에 있을수도, 아니면 S 바깥 즉 Preorder 집합 어딘가에 있을수도 있다. 예를 들어 정수 집합의 부분 집합인 S = {5, 8, 42, 34, 13943}에 대해서, Lower Bound는 5, 4 등이 될 수 있고 Upper Bound는 13943, 999999 등이 될 수 있다. (여기서 알 수 있는 사실 한 가지는 모든 자연수의 부분 집합은 최소 하나의 Lower Bound인 0을 갖는다는 것이다)

아무튼, 이처럼 원래 Upper Bound와 Lower Bound의 정의는, 어떤 집합의 부분 집합을 기준으로 생각하는 것이다.

C++ Standard Library

C++에는 std::lower_bound와 std::upper_bound라는 함수가 있는데, 이는 다음으로 설명 가능하다¹:

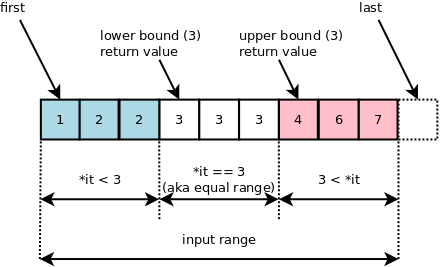
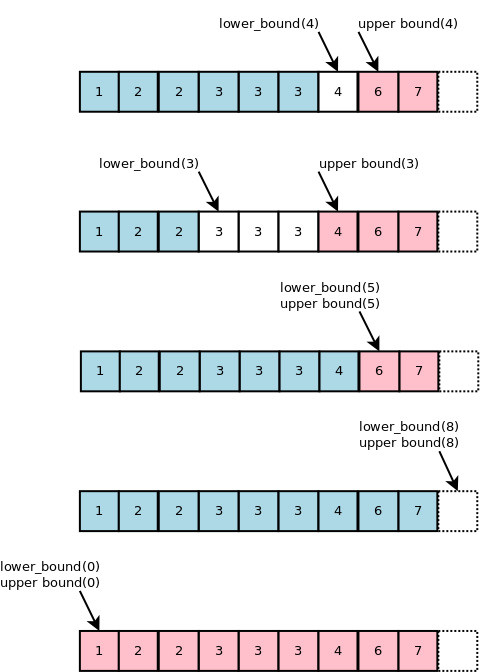
즉, 정렬된 배열 또는 리스트가 있고 어떤 값 x 를 기준으로 x가 구간(range)을 형성하는 경우에 std::upper_bound와 std::lower_bound는 다음과 같다.

• std::upper_bound: x보다 큰 값이 처음으로 나오는 위치
• std::lower_bound: x보다 크거나 같은 값이 처음으로 나오는 위치

뭔가 앞의 수학적 정의랑 비슷하면서도 다르다. 앞서 말했듯 수학적 정의는 어떤 집합의 부분 집합이 기준이었다. 이 기준을 구현에서 다음과 같이 생각해보면:

• 어떤 집합: 정렬된 배열 (또는 배열의 정렬된 일부 구간)
• 부분 집합: 찾고자 하는 값 x로 형성된 구간

이 관점에서 생각해 보면 std::lower_bound와 std::upper_bound가 하는 일은 수학적 정의와 관련이 있다. 한마디로 x가 형성하는 구간을 찾는 것이다. x가 형성하는 구간이 대상 배열 안에 존재한다면 수학적 의미의 (Greatest) Lower Bound와 (Least) Upper Bound 모두 x가 된다. 우리가 궁금한 것은 배열에서의 이 구간(인덱스)에 대한 정보이고, CS의 전통적인 Half-Closed Interval²을 따라 x 구간의 범위 [lower_bound, upper_bound)의 시작점과 끝점을 찾아주는 함수가 바로 std::lower_bound와 std::upper_bound인 것이다.

따라서, 이 정의를 활용하면 Upper Bound에는 x 보다 크거나 같은 값을 넣을 수 있고, Lower Bound에는 x 보다 작거나 같은 값을 넣을 수 있다. 좀더 쉽게 설명하면, 정렬된 배열에 x를 삽입하고 싶을 때, 정렬 순서를 유지한채로 넣을 수 있는 가장 첫 번째 위치가 Lower Bound이고 가장 마지막 위치가 Upper Bound 이다. 이때 삽입이란 해당 인덱스에 x를 넣고 원래 인덱스부터 나머지를 한칸씩 쭉 뒤로 밀어버리는 연산을 뜻한다.

참고로 파이썬에는 bisect라는 패키지가 있어서 곧바로 적용해볼 수 있다. std::lower_bound는 bisect.bisect_left와, std::upper_bound는 bisect.bisect_right 또는 bisect.bisect와 대응된다. 이때,

• Upper Bound를 ub(index)라고 한다면, arr[:ub] <= x < arr[ub:] 를 만족한다.
• Lower Bound를 lb(index)라고 한다면, arr[:lb] < x <= arr[lb:] 를 만족한다.

Bisection

def bisect_right(arr, x, low=0, high=None):
    """
    The return value idx is such that all element in arr[:idx] have elt <= x,
    and all elt in arr[idx:] have x < elt.
    So if x already appears in the list, arr.insert(x) will insert just after the rightmost
    x already there.
    """

    if low < 0:
        raise ValueError('low must be positive')

    if high is None:
        high = len(arr)

    # [low, high)
    while low < high:
        mid = (low + high) // 2

        if x < arr[mid]:
            high = mid
        else:
            low = mid + 1
    return low

def bisect_left(arr, x, low=0, high=None):
    """
    Return the index where to insert item x in a list arr, assuming arr is sorted.

    The return value idx is such that all element in arr[:idx] have elt < x,
    and all elt in arr[idx:] have x <= elt.
    So if x already appears in the list, arr.insert(x) will insert just after the leftmost
    x already there.
    """

    if low < 0:
        raise ValueError('low must be positive')

    if high is None:
        high = len(arr)

    # [low, high)
    while low < high:
        mid = (low + high) // 2

        if x <= arr[mid]:
            high = mid
        else:
            low = mid + 1
    return low