성능 엔지니어링 - 행렬 곱셈 이야기
목차
발단: 평소처럼 재미있는 글이 없나 하고 긱뉴스를 탐방하다가 컴파일러 엔지니어가 되는 법이라는 글을 보게 되었다. 한국에서만 컴파일러 관련 포지션이 적은건가 싶었는데 미국도 상황은 비슷한가보구나, 라고 생각하면서 읽다가, 저자의 추천으로 MIT OCW의 Performance Engineering 강의를 만나게 되었다. 마침 최근 내 관심사와 맞닿아 있는 주제라서 강의 슬라이드를 보고 있는데 너무 재밌어서 내 식으로 소화도 할 겸 좀 정리해보려고 한다. 마침 MIT OpenCourseWare 라이센스도 출처만 표기한다면 너그러운 편이다.
1강은 성능 엔지니어링 전반에 대한 이야기를 시작으로, 행렬 곱셈을 어디까지 최적화할 수 있는지에 대한 이야기이다.
성능
소프트웨어를 만들 때는 성능보다 더 중요하게 고려해야 하는 속성들이 있다. 호환이 잘 되는지, 올바르게 동작하는지, 원하는 기능이 잘 동작하는지, 신뢰도는 어떤지, 코드는 분명한지, 유지보수는 얼마나 용이한지, 다른 모듈과의 조립은 얼마나 용이한지, 이식성은 좋은지, 테스트하기 좋은지, 사용성이 좋은지, 디버깅하기 좋은지, 강건한지(Robustness) 등등.
성능은 이러한 속성을 “살 수 있는” 일종의 화폐라고 볼 수 있다. 즉, 우리는 성능을 희생해서 유지보수성을 높일 수 있고, 성능을 희생해서 디버깅하기 좋은 코드를 만들 수 있고, 성능을 희생해서 모듈성을 높일 수 있다. 그러니까 소프트웨어 엔지니어링의 모든 분야가 늘 그렇듯 균형(Trade-Off)을 고려해야만 한다.
아주 초창기 컴퓨팅 하드웨어의 파워가 빈약했던 시절에는 하드웨어의 비용 문제도 있었지만, 일정 수준의 성능이 받쳐주지 않으면 애초에 프로그램 자체를 돌릴 수 없는 경우도 많았다. 그래서 이 시절에는 앞서 말한 소프트웨어의 다양한 중요한 속성들을 많이 희생하면서 성능에 집중하기도 했다. 그러다보니 섣부른 최적화와 관련해서 많은 교훈들이 알려져 있다.
Premature optimization is the root of all evil. - Donald Knuth
아마도 도널드 크누스의 이 문장이 가장 유명할 것이다. 섣불리 최적화하면 큰일난다.
More computing sins are committed in the name of efficiency (without necessarily achieving it) than for any other single reason - including blind stupidity. - William Wulf
이 말은 72년에 ACM 컨퍼런스에서 발표된 논문 “A Case Against the GOTO” 에서 나온 말이다. 교과서에서 배웠던 “GOTO 쓰지마세요”를 주장한 논문이라고 한다. 실제로 성능 개선을 이루지 못하면서도 효율성이라는 이름 하에 저질러지는 나쁜 프로그래밍 관행이 아주 많으니, 효율성을 과도하게 쫓지 말라는 경고를 담고 있다.
(Jackson’s Rules of Optimization) The first rule of program optimization: Don’t do it. The second rule of program optimization - for experts only: don’t do it yet. - Michael Jackson
마이클 잭슨은 낚시가 아니라 영국의 컴퓨터 과학자 마이클 A. 잭슨이다. 잭슨의 최적화 규칙으로 알려진 이 말은 초기의 과도한 최적화가 코드의 복잡성을 높이고 버그를 유발하니까 되도록 피하고 나중에 필요한 부분만 최적화하라는 교훈을 담고 있다.
그런데 무어의 법칙에 따라 시간이 지나면서 하드웨어, 특히 단일 칩의 성능이 비약적으로 발전하기 시작했다. 비유하자면 성능이라는 화폐를 마구 찍어내는 시기였다. 하지만 그것도 2004년까지였고, 그 이후에는 물리적인 한계로 인해 프로세서의 클럭 스피드가 예전만큼 극적으로 증가하지는 않게 되었다.
그래서 하드웨어 제조사들은 단일 칩의 성능을 개선하는 것에서 벗어나서 여러 개의 코어를 탑재하는 쪽으로 눈을 돌렸다. 성능의 규모를 늘리기 위해서 (scale), 여러 개의 코어를 마이크로 프로세서 칩에 박기 시작한 것이다. 물론 단일 칩의 성능도 꾸준히 좋아지고는 있지만, 이제 옛날처럼 성능이라는 화폐를 마구 찍어낼 수는 없다. 더 이상 성능은 공짜가 아니다.
현대의 멀티코어 프로세서는 그 이름대로 여러 개의 병렬 처리 코어를 담고, 복잡한 캐시 구조와, 병렬 처리를 위한 벡터 하드웨어와, 프리 페처와, 하이퍼쓰레딩, 등등 많은 것들을 탑재하기 시작했다. 그리고 이런 복잡한 하드웨어의 성능을 최대한 이끌어내려면 소프트웨어를 반드시 거기에 맞춰야 한다. 즉, 성능을 위한 엔지니어링이 필요하다.
당연하지만 이런 성능 엔지니어링은 어렵다. 어떻게 하면 현대의 하드웨어를 효과적으로 활용할 수 있는 소프트웨어를 짤 수 있을까? 이것이 바로 성능 엔지니어링의 핵심 질문이다.
행렬 곱셈 문제
성능 엔지니어링을 통해서 현대의 멀티코어 하드웨어의 성능을 어디까지 끌어낼 수 있을지, 행렬 곱셈 문제를 중심으로 살펴보자. 여기서는 다음과 같은 단순한 곱셈 식을 중심으로 살펴볼 것이다.
\[\begin{bmatrix} c_{11} & c_{12} & \cdots & c_{1n} \\ c_{21} & c_{22} & \cdots & c_{2n} \\ \vdots & \vdots & \ddots & \vdots & \\ c_{n1} & c_{n2} & \cdots & c_{nn} \\ \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots & \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{bmatrix} \cdot \begin{bmatrix} b_{11} & b_{12} & \cdots & b_{1n} \\ b_{21} & b_{22} & \cdots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots & \\ b_{n1} & b_{n2} & \cdots & b_{nn} \\ \end{bmatrix}\] \[c_{ij} = \Sigma^{n}_{k=1} a_{ik} b_{kj}\]문제를 심플하게 하기 위해서 \(n = 2^{12} = 4096\) 라고 하자.
실험할 하드웨어
실험하기 좋은 세상이다. 클라우드가 도처에 널려있다. 가장 유명한 AWS의 c4.8xlarge 머신의 스펙은 다음과 같다. (아마도 옛날 기준인듯 하다, 지금은 스펙이 다를듯)
| 상세 | 스펙 |
|---|---|
| 마이크로아키텍쳐 | 하스웰 (인텔 제온 E5-2666 v3) |
| 클럭 속도 | 2.9 GHz |
| 프로세서 칩 수 | 2 |
| 프로세싱 코어 수 | 프로세서 칩 당 9 |
| 하이퍼스레딩 | 2-way |
| 부동 소수점 유닛 | 각 코어가 한 사이클마다 8개의 배정밀도 연산 가능 |
| 캐시 라인 크기 | 64B |
| L1 인스트럭션 캐시 | 32KB private 8-way set associative |
| L1 데이터 캐시 | 32KB private 8-way set associative |
| L2 캐시 | 256KB private 8-way set associative |
| L3 캐시 (LLC) | 25MB shared 20-way set associative |
| DRAM | 60GB |
사실 나는 위의 하드웨어 스펙만 봐서는 이게 어떤 의미인지 잘 모르겠어서 조금 더 찾아봤다.
- 마이크로아키텍쳐: 하스웰은 2013년에 출시했다. 강의 슬라이드 날짜인 2018년 기준으로도 최신은 아니지만, 안정적이고 전력 효율이 좋다고 한다.
- 클럭 속도 (Clock Frequency): GHz니까 초당 29억 번 (\(2.9 \times 10^{9}\)) 연산(사이클)을 할 수 있다.
- 프로세서 칩 수: 2개의 물리 프로세서 칩이 이 프로세서에 박혀있다는 뜻이다.
- 프로세싱 코어 수: 위의 물리 칩 하나 당 9개의 코어가 있다는 뜻이다. 그래서 총 18개의 물리 코어가 있다.
- 하이퍼스레딩: 각 물리 코어에서는 최대 2개의 쓰레드를 동시에 실행할 수 있다는 뜻이다. 그래서 총 36개의 가상 코어가 있다.
- 부동 소수점 유닛: 원문은 “8 double-precision operations, including fused-multiply-add, per core per cycle” 이라고 되어 있는데, 이거만 봐서는 잘 이해가 안되어서 좀더 찾아봤다. 일단 FMA(Fused-Multiply-Add) 라는 건 곱셈과 덧셈을 한 사이클에 수행하게 해주는 기능이다. 그리고 배정밀도(double-precision)는 64비트의 부동 소수점을 의미한다. “per core per cycle”라는 말이 가장 헷갈렸는데, 앞문장과 합쳐서, 이는 각각의 코어가 한 클럭 사이클마다 최대 8개의 배정밀도 연산이 가능하다는 뜻이다. 참고로 이건 물리적으로 8개의 FPU가 달려있다는 뜻이 아니다. 하스웰에는 AVX (Advanced Vector Extensions) 라는 명령어가 제공되는데, 이를 통해 256비트 벡터에 대한 부동 소수점 연산을 한 사이클에 처리할 수 있다. 이걸 배정밀도 기준으로 쪼개면 4개인데, FMA를 통해서 덧셈과 곱셉을 한번에 할 수 있으니, 총 8개의 배정밀도 부동 소수점 연산(그래서 모호하게 연산 이라고 쓴 것 같다)이 가능하다는 의미로 해석된다. 즉, 하드웨어가 제공하는 고급 명령어를 이용하면, 각 코어마다 부동 소수점 연산의 처리량을 한 사이클에 최대 8배 더 할 수 있다는 뜻이다. 어차피 우리는 유닛의 개수가 몇 개인지가 중요한게 아니라 처리량이 중요하기 때문에 이 정보가 더 의미있다.
- 캐시 라인 크기: 메모리에서 한 번에 가져오는 데이터 단위이다. 이 크기만큼 캐시에 로드된다.
- L1 캐시들: 가상 메모리 이야기의 인트로에서 잠깐 살펴봤듯, 인스트럭션 캐시와 데이터 캐시로 나뉘어져있는 것을 알 수 있다. 32KB는 크기이고, private은 하나의 물리 코어가 독점적으로 하나 씩 갖고 있다는 의미이다. 그래서 총 18개의 L1 인스트럭션 캐시와 18개의 L1 데이터 캐시가 붙어 있다. 8-way set associative는 캐시의 주소 맵핑 방식 중 하나인데, 이건 다음 기회에 조금 더 자세히 살펴보려고 한다. 아무튼 중요한 건 매우 빠르다.
- L2 캐시: 역시 코어마다 전용으로 붙어 있으므로 (private) 총 18개가 있고, 사이즈도 더 크지만, L1보다는 느리다.
- L3 캐시: LLC는 Last Level Cache라는 뜻이다. 즉 여기까지만 캐시가 붙고 이후는 메모리 접근이라서 많이 느리다. shared의 기준은 칩이라서 총 2개의 L3가 붙어 있고 칩 안의 모든 9개 코어가 공유한다.
그럼 이 하드웨어 스펙으로부터 뭘 알아 낼 수 있냐면, 이상적인 조건에서 달성 가능한 최대 성능을 계산해볼 수 있다. 특히 요즘 AI로 인해서 화두가 되고 있는 GFLOPS(기가플롭스; 초당 부동 소수점 연산의 수), 그 중에서도 이론적으로 가능한 Peak GFLOPS를 계산할 수 있다.
- Peak GFLOPS = 클럭 속도 x 물리 코어 수 x 싸이클 당 부동 소수점 연산 수 x 하이퍼스레딩 팩터
- 이를 계산하면 \((2.9 \times 10^9) \times 2 \times 9 \times 16\)로 대략 836 GFLOPS를 얻는다.
여기서 하이퍼스레딩 팩터는 하이퍼스레딩 2 way와 8배의 배정밀도 부동소수점 연산 처리량을 모두 고려한 값이다. 클럭은 초당 사이클 수 이고, 8배의 연산 처리량은 코어마다 한 사이클에 최대 8개의 배정밀도 연산이 가능하다는 의미이니 8을 곱하는 데에는 의심의 여지가 없다. 다만 2-way 하이퍼스레딩이라서 2를 곱한 것은 조금 의문이 있다. 왜냐하면 2-way 하이퍼스레딩은 물리적으로 2개의 연산 유닛이 붙어 있다는 뜻이 아니라 두 개의 논리적인 쓰레드를 동시에 실행할 수 있다는 의미라서, Peak GFLOPS를 계산할 때는 물리 코어만 고려해야하지 않나 하는게 내 생각이다. 아주 이상적인 실행 환경에서는 2를 곱하는게 맞겠지만, 실제로는 달성 불가능하지 않을까. 아무튼 강의 슬라이드에서는 2를 곱한 이상적인 값을 기준으로 했으니 일단 여기서도 똑같이 하고자 한다.
그러면 이제 이상적인 최대 성능인 Peak GFLOPS를 기준으로, 각각의 프로그래밍 언어와 방법에 따라서 우리가 얼마나 이 하드웨어를 활용할 수 있는지 살펴보자.
버전 1: 파이썬
import sys, random
from time import *
n = 2 ** 12
A = [[random.random() for _ in range(n)] for _ in range(n)]
B = [[random.random() for _ in range(n)] for _ in range(n)]
C = [[0 for _ in range(n)] for _ in range(n)]
start = time()
for i in range(n):
for j in range(n):
for k in range(n):
C[i][j] += A[i][k] * B[k][j]
end = time()
print(f"{end - start:.6f}")
앞에서 봤던 행렬 곱셈에 대한 element-wise 식인 \(c_{ij} = \Sigma^{n}_{k=1} a_{ik} b_{kj}\) 를 나이브하게 구현한 파이썬 코드이다. 당연히 순수 파이썬이라서 느리겠지만, 이게 얼마나 느린 걸까?
위의 실험 머신에서 이걸 돌리면 21,042초, 약 6시간 정도가 걸린다고 한다. 우리는 머신의 이론적인 Peak GFLOPS가 836 이라는 사실을 계산했다. 파이썬 코드가 얻은 FLOPS를 러프하게 계산해보자.
먼저 \(n^3\)번의 반복문 안에서 곱셈과 덧셈을 하고 있으니, 총 \(2 \times n^3 = 2 \times (2 ^{12}) ^{3} = 2^{37}\) 번의 부동 소수점 연산을 한다 (FLOP). 그리고 이 연산을 다 하는데 21,042 초가 걸렸으니, 최종 FLOPS는 \(2^{37} / 21042 \approx 6.25 \text{ MFLOPS}\) 가 된다. Peak GFLOPS에 대한 비율을 계산해보면, 이 프로그램은 최대 성능 대비 \(\frac{6.25 \times 10^6}{836 \times 10^9} \approx\) 0.00078% 밖에 뽑아내지 못한다는 사실을 알 수 있다. 순수 파이썬이 느리다는 사실은 익히 들어 알고 있지만, 이렇게 수치를 통해서 비교해보니 더더욱 처참한 수치이다.
버전 2: 자바
import java.util.Random;
public class mm_java {
static int n = 4096;
static double[][] A = new doulble [n][n];
static double[][] B = new doulble [n][n];
static double[][] C = new doulble [n][n];
public static void main(String[] args) {
Random r = new Random();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
A[i][j] = r.nextDouble();
B[i][j] = r.nextDouble();
C[i][j] = 0;
}
}
long start = System.nanoTime();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
C[i][j] += A[i][k] * B[k][j;]
}
}
}
long end = System.nanoTime();
double elapsed = (end - start) * 1e-9;
System.out.println(elapsed);
}
}
역시 동일한 머신에서 수행하면, 이 자바 코드는 2,738초로 약 46분이 걸린다. 파이썬보다 7.7배는 빠르지만, 여전히 최대 성능 대비 0.006% 밖에 안된다.
버전 3: C
#include <stdio.h>
#include <stdlib.h>
#include <sys/time.h>
#define n 4096
double A[n][n];
double B[n][n];
double C[n][n];
float elapsed(struct timeval *start, struct timeval *end) {
return (end->tv_sec - start->tv_sec) + 1e-6 * (end->tv_usec - start->tv_usec);
}
int main(int argc, const char* argv[]) {
for (int i = 0; i < n; i++){
for (int j = 0; j < n; j++) {
A[i][j] = (double) rand() / (double) RAND_MAX;
B[i][j] = (double) rand() / (double) RAND_MAX;
C[i][j] = 0.0;
}
}
struct timeval start, end;
gettimeofday(&start, NULL);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
gettimeofday(&end, NULL);
printf("%0.6f\n", elapsed(&start, &end));
return 0;
}
Clang/LLVM 5.0 컴파일러를 이용하면 대략 1,156초로 약 19분이 걸린다. 대충 자바보다 2배, 파이썬보다 18배 빠르지만 그래도 여전히 최대 성능 대비 0.014%다.
여기까지는 프로그래밍 언어 간의 성능 차이를 확인할 수 있었다. 정적 타입 언어이자 머신 코드로 컴파일되어 곧바로 실행되는 C는, 동적 타입 언어이자 인터프리터를 통해 실행되는 파이썬에 비해서 18배나 빠르다. 그럼에도 여전히 우리가 계산한 이상적인 성능에는 발끝도 미치지 못한다. 그러면 이제 뭘 더 해볼 수 있을까?
버전 4: 반복문 중첩 순서 바꾸기
이제부터 시도해볼 최적화는 모두 가장 빨랐던 C 프로그램을 기준으로 한다. 먼저 코드의 정확성을 희생하지 않고 반복문이 중첩되는 순서를 바꿔볼 수 있다. i, j, k 총 3개의 반복문이 있으므로 순서를 고려하면 총 6개의 반복문 순서를 얻을 수 있다. 각각을 실행해보면 다음과 같다.
| 반복 순서 (바깥쪽 -> 안쪽) | 수행 시간 (초) |
|---|---|
| i -> j -> k | 1155.77 |
| i -> k -> j | 177.68 |
| j -> i -> k | 1080.61 |
| j -> k -> i | 3056.63 |
| k -> i -> j | 179.21 |
| k -> j -> i | 3032.82 |
순서만 바꿨을 뿐인데 가장 빠른 것과 가장 느린 것의 차이가 17배나 된다!
대체 왜 이런 일이 가능한지를 이해하려면 메모리가 동작하는 방식을 알아야 한다. 단일 칩의 성능 개선이 점차 어려워지자 많은 제조사들은 멀티코어로 눈을 돌렸는데, 이로 인해 성능은 단일 칩의 연산 속도보다는 여러 개의 코어가 얼마나 잘 협동하는지, 특히 그 과정에서 해야 할 작업을 얼마나 효율적으로 공유하고 있는지에 더 큰 영향을 받게 되었다. 즉, 메모리에 어떻게 접근하는지, 특히 여러 번 쓰이는 연속된 메모리 블럭을 최대한 캐시에 잘 붙들여 놓는 것이 중요하다.
우리의 행렬 곱셈 케이스에서, 각 행렬은 메모리에 행 우선 순서 (row-major order) 로 올라가있다. 즉, 다음과 같은 행렬이 있을 때:
\[\begin{bmatrix} Row 1 (= x_{1,1} x_{1,2} \cdots x_{1,N})\\ Row 2 (= x_{2,1} x_{2,2} \cdots x_{2,N})\\ \cdots \\ Row N (= x_{N,1} x_{N,2} \cdots x_{N,N})\\ \end{bmatrix}\]이 행렬은 메모리에 다음과 같은 연속된 모양으로 올라간다.
\[\begin{bmatrix} Row 1 & Row 2 & \cdots & Row N \end{bmatrix}\]그러면 우리가 처음에 구현했던 순서인 i -> j -> k (1155.77초)를 다시 살펴보자.
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
for (int k = 0; k < n; k++)
C[i][j] += A[i][k] * B[k][j];
- C: 어차피 제일 안쪽 반복문(k) 안에서 접근하는 C의 원소는 한 군데 (i, j) 뿐이다. 공간 지역성이 아주 좋다.
- A: A[i] 행에 대해서 0부터 k까지 순차적으로 접근한다. 공간 지역성이 좋다.
- B: 공간 지역성이 최악이다. B[0] 번째 행의 j번째 원소부터, B[k] 번째 행의 j번쨰 원소까지 접근해야 한다. 그러면 B[0][j]에 접근한 후 B[1][j]에 접근하려면 4096개의 연속된 블럭 메모리를 뛰어넘어가야 한다.
제일 빨랐던 i -> k -> j (117.68초) 는 어떨까?
for (int i = 0; i < n; i++)
for (int k = 0; k < n; k++)
for (int j = 0; j < n; j++)
C[i][j] += A[i][k] * B[k][j];
- C: 이제 가장 안쪽 반복문은 j다. C[i] 번째 행의 0부터 j번째 원소까지 접근하므로 공간 지역성이 훌륭하다.
- A: 가장 안쪽 반복문 j에서 접근하는 A의 원소는 (i, k) 한 군데 뿐이다. 최고다.
- B: 이제 B의 공간 지역성도 훌륭하다. B[k] 번째 행의 0부터 j번째 원소까지를 순차적으로 접근한다.
말이 되는 설명이다. 그러면 실제로는 어떨까? 모든 성능 엔지니어링은 수치를 직접 눈으로 확인하는 프로파일링 과정이 필수적이다. 캐시의 효과를 살펴보기 위해서는 우리는 valgrind 프로그램에 --tool=cachegrind 옵션을 줘서, 캐시의 성능을 시뮬레이션해볼 수 있다1 2. 그러면 앞선 테이블에 추가로 하나의 컬럼을 다음과 같이 추가할 수 있다.
| 반복 순서 (바깥쪽 -> 안쪽) | 수행 시간 (초) | LLC 미스 율 |
|---|---|---|
| i -> j -> k | 1155.77 | 7.7% |
| i -> k -> j | 177.68 | 1.0% |
| j -> i -> k | 1080.61 | 8.6% |
| j -> k -> i | 3056.63 | 15.4% |
| k -> i -> j | 179.21 | 1.0% |
| k -> j -> i | 3032.82 | 15.4% |
즉, 가장 안쪽 루프에서, 가장 공통된 가장 안쪽 인덱스인 j를 순차적으로 접근하기만 하면, 가장 최적으로 LLC을 활용할 수 있고, 다시 말해 최적의 메모리 접근 지역성을 통해 가장 좋은 성능을 낼 수 있다. 테이블에서 확인할 수 있듯이 가장 안쪽 반복문이 j이기만 하면 i -> k -> j 이든 k -> i -> j 이든 미스 율은 동일하게 1.0% 인 것을 확인할 수 있다. 2초정도의 차이는 오차 범위 이내다.
하지만, 그럼에도 177.68초라는 시간이 걸렸고, 이는 이상적인 최대 성능 대비 0.093% 밖에 되지 않는다.
버전 5: 컴파일러 최적화
C 컴파일러는 프로그램의 원래 의미를 해치지 않는 선에서 여러 가지 단계의 최적화 플래그를 제공한다.
-O0: 최적화 안함-O1: 적당히 최적화 함-O2: 많이 최적화함-O3: 공격적으로 최적화함, 컴파일 시간이 오래 걸리고 코드 크기가 늘어남
보통 프로덕션에 통용되는 최적화 레벨은 -O2까지인 것 같다. -O3는 아주 특수한 케이스가 아니면 잘 쓰지 않는다. 아무튼 j를 마지막에 접근하는 프로그램에 각각의 최적화 플래그를 적용해보면 다음과 같이 또 약간의 성능을 얻는다.
| 최적화 플래그 | 수행 시간 (초) |
|---|---|
-O0 |
177.68 |
-O1 |
66.24 |
-O2 |
54.63 |
-O3 |
55.58 |
하지만, 그럼에도 54.63초가 걸렸고, 이는 이상적인 최대 성능 대비 0.301% 밖에 안된다.
버전 6: 병렬 처리
대체 뭐가 성능을 가로막고 있는 걸까?
앞에서 살펴본 우리의 하드웨어는 분명 18개의 물리 코어를 갖고 있다고 했지만, 우리는 지금까지 단 하나의 코어만 사용하고 있었다. 나머지 17개의 물리 코어는 놀고 있었다! 얘네들을 쉼없이 일하게 시켜야 한다.
병렬 처리를 위한 다양한 라이브러리가 있지만, 여기서는 MIT에서 만든 Cilk를 쓴다 (당연하다; MIT 교육이니). Cilk는 C/C++ 언어를 확장하여 병렬로 처리할 작업을 논리적으로 쉽게 표현할 수 있도록 해준다. 그 중에서도 cilk_for를 이용하면 for와 유사한 문법 구조를 따르면서도 반복문을 직접 물리 코어에다가 병렬로 수행하게 할 수 있다.
앞에서 반복문의 접근 순서에 따라 속도가 달라졌듯이, 어떤 반복문을 병렬로 수행할 것인지도 성능에 영향을 미친다. 가장 빨랐던 i -> k -> j 를 기준으로 생각해보자. 일단 k는 병렬화 할 수 없다. 왜냐하면 같은 i, j 조합에 대해서 계속 누적되기 때문이다.
- k=0 일 때:
C[i][j] += A[i][0] * B[0][j] - k=1 일 때:
C[i][j] += A[i][1] * B[1][j] - k=2 일 때:
C[i][j] += A[i][2] * B[2][j]
즉, 이렇게 순차적인 의존성이 있을 때는 병렬로 수행할 수 없다.
그러면 i와 j에 대해서면 병렬 반복인 cilk_for를 적용해볼 수 있다. 어떤 걸 적용해야할까? 모든 3개의 조합을 시도해보면 다음과 같은 결과를 얻는다.
cilk_for 적용 루프 |
수행 시간 (초) |
|---|---|
| i | 3.18 |
| j | 531.71 |
| i, j | 10.64 |
즉, 안쪽 루프보다는 바깥쪽 루프를 병렬 처리하는 것이 좋다. 왜냐하면 가장 큰 병렬성(n개의 독립적 작업)을 얻기 때문이다. 그리고 앞에서 고려한 캐시 지역성(cache locality)을 더 잘 활용한다. 헷갈리면 그냥 가장 바깥쪽 루프만 병렬처리 하면 된다.
cilk_for (int i = 0; i < n; i++)
for (int k = 0; k < n; k++)
for (int j = 0; j < n; j++)
C[i][j] += A[i][k] * B[k][j];
최종 코드는 위와 같다. 이렇게 3.18초, 최대 성능 대비 5.17%를 끌어내었다. 드디어 한 자릿 수까지 왔다. 참고로 이 수치는 18개의 물리 코어를 모두 활용해서 얻은 수치이며, 병렬 처리를 하지 않은 버전 대비 약 18배 빠르다.
버전 7: 메모리 접근 최적화
이제 우리 프로그램은 타입을 컴파일 타임에 알아내어서 머신 코드로 바로 실행되는 바이너리로 컴파일되고, 공간 지역성도 잘 지켰고, 컴파일러 최적화도 했고, 모든 18개의 물리 코어를 다 쓰도록 했다. 사실 여기까지가 내가 그동안 알고 있던 최적화의 내용이기도 하다. 그런데도 왜 여전히 최대 성능의 5% 밖에 안되는 걸까? 어떻게 하면 하드웨어의 고급 기능을 다 활용할 수 있을까?
사실 우리는 아직까지 하드웨어 캐시를 다 활용하고 있지 못하다. 데이터를 최대한 재사용하도록 계산의 구조를 재정렬하면 캐시 미스를 최소한으로 줄이고 캐시 히트를 최대한 늘릴 수 있다.
성능 엔지니어링에서 중요한 것은 프로파일링, 수치를 계산해보고 눈으로 확인하는 일이다. 먼저, 행렬 C의 행 하나를 전부 계산하기 위해서 반복문 코드가 메모리 접근을 몇 번 해야하는지를 계산해보자.
- 4096 \(\times\) 1 = 4096 번 C에 쓰기 작업이 필요하고,
- 4096 \(\times\) 1 = 4096 번 A에서 읽기 잡업이 필요하고,
- 4096 \(\times\) 4096 = 16,777,216 번 B에서 읽기 작업이 필요하다.
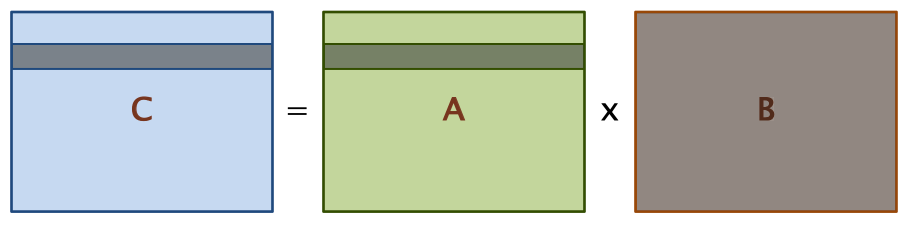
따라서 총 16,785,408 번의 메모리 접근이 발생한다.
데이터를 재사용하려면 메모리에 어떤 식으로 접근해야 할까? 행렬 C를 계산할 때 행 하나가 아니라, 64x64 크기의 타일로 접근한다고 해보자.
- 64 \(\times\) 64 (타일 크기) = 4096 번 C에 쓰기 작업이 필요하고,
- 64 \(\times\) 4096 = 262,144 번 A에서 읽어야 하고,
- 4096 \(\times\) 64 = 262,144 번 B에서 읽어야 한다.
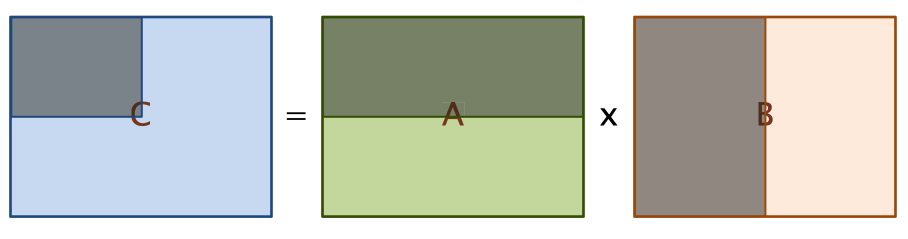
따라서 총 528,384 번의 메모리 접근이 필요하다.
오호. 분명 같은 계산을 하는데, 어떤 부분을 먼저 하느냐에 따라서 메모리 접근 횟수가 줄었다. 알고리즘 시간에 배웠던 분할 정복의 위력을 눈으로 확인한 순간이다. 역시 이 타일의 크기도 바꿔볼 수 있으니, 이걸 조절할 수 있도록 정사각형 타일의 크기를 s라고 했을 때, 나이브하게는 다음과 같이 구현할 수 있다.
for (int ih = 0; ih < n; ih += s)
for (int jh = 0; jh < n; jh += s)
for (int kh = 0; kh < n; kh += s)
for (int il = 0; il < s; il++)
for (int kl = 0; kl < s; kl++)
for (int jl = 0; jl < s; jl++)
C[ih + il][jh + jl] += A[ih + il][kh + kl] * B[kh + kl][jh + jl];
이 코드는 몇 가지 생각할 부분이 있다.
- 인덱스를 두 단계, high와 low로 나누어서, 예를 들어 원래 인덱스인 i를 ih에 il를 더해서 접근하게 만들고, high의 크기를 우리가 원하는 타일의 크기인 s로 설정한다. 이렇게 하면 가장 바깥쪽 루프는 타일 크기만큼 뛰어넘으면서, 안쪽 루프는 그 타일 안에서 low 인덱스를 1씩 증가하여 접근할 수 있다.
- 안쪽 반복문의 접근 순서는 우리가 찾아내었던 가장 빠른 순서인 i -> k -> j 그대로인데, 바깥쪽 반복문은 i -> j -> k이다.
- 이전과 마찬가지로 k는 병렬화가 불가능하다. 가장 최적은 바깥쪽 i, j 두개만 병렬화 하는 것.
그래서 위 코드를 Cilk로 병렬화 하면 다음과 같다.
cilk_for (int ih = 0; ih < n; ih += s)
cilk_for (int jh = 0; jh < n; jh += s)
for (int kh = 0; kh < n; kh += s)
for (int il = 0; il < s; il++)
for (int kl = 0; kl < s; kl++)
for (int jl = 0; jl < s; jl++)
C[ih + il][jh + jl] += A[ih + il][kh + kl] * B[kh + kl][jh + jl];
이전과 비슷하게 이번에도 타일 크기 s를 조절해가면서 실험을 해볼 수 있다.
| 타일 크기 | 수행 시간 (초) |
|---|---|
| 4 | 6.74 |
| 8 | 2.76 |
| 16 | 2.49 |
| 32 | 1.74 |
| 64 | 2.33 |
| 128 | 2.13 |
타일 크기가 32일 때 수행 시간도 절반 가까이로 줄어든 것을 볼 수 있다. 참고로 이 32라는 타일 크기는 항상 통용되는 값이 아니라, 문제에 따라 조절해야 하는 파라미터이다. 최적의 성능을 위한 값은 이렇게 실험을 통해 알아내는 수 밖에 없다. 아무튼 이렇게 최대 성능의 9.45%를 끌어내었다.
참고로 타일링은 같은 개수의 원소를 계산하는데 필요한 메모리 접근 횟수만 줄이는게 아니라, 캐시 히트율도 엄청나게 올린다. 버전 6에서 그냥 Cilk를 적용한 것과 이번 버전에서 타일링을 적용한 것 각각의 캐시 성능을 비교하면, LLC 기준으로 95%의 성능 향상을 볼 수 있다.
| 버전 | 캐시 레퍼런스 (백만) | L1 데이터 캐시 미스 (백만) | LLC 미스 (백만) |
|---|---|---|---|
| 버전 6 (병렬 처리 ) | 104,090 | 17,220 | 8,600 |
| 버전 7 (타일링) | 64,690 | 11,777 | 416 |
버전 8: 병렬로 분할정복
현대 멀티 코어 프로세서의 캐시 및 메모리 구조를 조금만 더 자세히 살펴보자.
| 단계 | 크기 | 정보 | 레이턴시 (ns) |
|---|---|---|---|
| 메인 메모리 | 60GB | 50 | |
| LLC (L3) | 25MB | 20-way, shared | 12 |
| L2 | 256KB | 8-way, private | 4 |
| L1-d | 32KB | 8-way, private | 2 |
| L1-i | 32KB | 8-way, private | 2 |
코어들 간에 공유되는 LLC를 제외하면, 코어 독접적 캐시는 L1, L2 총 두 개가 있고 이 둘은 다른 캐시에 비해서 매우매우 빠르다 (order of magnitude). 따라서 이 두 캐시를 최대한 활용하는 것이 성능 엔지니어링에 있어 필수적이다.
어떻게 하면 좋을까? 핵심 아이디어는 알고리즘 시간에 배웠던 분할 정복을 떠올리는 것이다. 타일링을 항상 같은 크기인 s로 하는 것이 아니라, 2의 모든 거듭 제곱 크기에 대해서 동시에 타일링을 진행한다. 예를 들어 NxN 행렬의 곱셈 문제를 다음과 같이 N/2xN/2 행렬을 8번 곱한 다음 NxN 행렬을 한번 더하는 문제로 바꾸면, 부분 문제인 N/2xN/2의 곱셈이 결국 타일링과 같아진다. 그리고 이걸 재귀적으로 적용해서 타일링된 행렬의 곱셈 역시 타일링하여 계산하게 되면, 메모리 접근 성능과 캐시 활용을 극적으로 끌어올릴 수 있다. 추가로 이렇게 N/2xN/2로 쪼갠 부분 문제들은 서로 의존성이 없기 때문에, 이 부분 문제들을 풀 때 병렬 처리를 적극 적용할 수 있게 된다.
\[\begin{align*} \begin{bmatrix} C_{0,0} & C_{0,1} \\ C_{1,0} & C_{1,1} \\ \end{bmatrix} &= \begin{bmatrix} A_{0,0} & A_{0,1} \\ A_{1,0} & A_{1,1} \\ \end{bmatrix} \times \begin{bmatrix} B_{0,0} & B_{0,1} \\ B_{1,0} & B_{1,1} \\ \end{bmatrix} \\ &= \begin{bmatrix} A_{0,0}B_{0,0} & A_{0,0}B_{0,1} \\ A_{1,0}B_{0,0} & A_{1,0}B_{0,1} \\ \end{bmatrix} + \begin{bmatrix} A_{0,1}B_{1,0} & A_{0,1}B_{1,1} \\ A_{1,1}B_{1,0} & A_{1,1}B_{1,1} \\ \end{bmatrix} \\ \end{align*}\]이렇게 문제를 쪼개면 결국 가장 풀기 쉬운 부분 문제인 기저 조건 (Base Case) 까지 닿게 된다. 그런데 기저 조건의 크기가 너무 작으면, 즉 문제를 너무 잘게 쪼개면 오히려 성능이 떨어질 수도 있다. 그러므로 이 접근에서 튜닝할 수 있는 파라미터는 기저 조건의 크기가 된다. 따라서, 구현은 다음과 같이 된다.
void mm_base(
double *restrict C, int n_C,
double *restrict A, int n_A,
double *restrict B, int n_B,
int n) {
for (int i = 0; i < n; i++)
for (int k = 0; k < n; k++)
for (int j = 0; j < n; j++)
C[n_C * i + j] += A[n_A * i + k] * B[n_B * k + j];
}
void mm_dac(
double *restrict C, int n_C,
double *restrict A, int n_A,
double *restrict B, int n_B,
int n) {
// C += A * B
if (n <= THRESHOLD) {
mm_base (C, n_C, A, n_A, B, n_B, n);
} else {
#define X(M,r,c) (M + (r*(n_ ## M) + c)*(n/2))
cilk_spawn mm_dac(X(C,0,0), n_C, X(A,0,0), n_A, X(B,0,0), n_B, n/2);
cilk_spawn mm_dac(X(C,0,1), n_C, X(A,0,0), n_A, X(B,0,1), n_B, n/2);
cilk_spawn mm_dac(X(C,1,0), n_C, X(A,1,0), n_A, X(B,0,0), n_B, n/2);
mm_dac(X(C,1,1), n_C, X(A,1,0), n_A, X(B,0,1), n_B, n/2);
cilk_sync;
cilk_spawn mm_dac(X(C,0,0), n_C, X(A,0,1), n_A, X(B,1,0), n_B, n/2);
cilk_spawn mm_dac(X(C,0,1), n_C, X(A,0,1), n_A, X(B,1,1), n_B, n/2);
cilk_spawn mm_dac(X(C,1,0), n_C, X(A,1,1), n_A, X(B,1,0), n_B, n/2);
mm_dac(X(C,1,1), n_C, X(A,1,1), n_A, X(B,1,1), n_B, n/2);
cilk_sync;
}
}
restrict키워드는 포인터가 메모리의 겹치지 않는 영역만을 가리킨다는 것을 컴파일러에게 알려준다. 즉, 포인터 알리아싱이 없다는 것을 컴파일러에게 힌트로 보장해주어서 추가적인 최적화가 가능하게 한다.- 기저 사례를 처리하는
mm_base함수는 특정 임계 크기 이하일 때 직접 곱셈을 수행하는 역할을 한다. 이 값이 메모리 연산에 적절한 크기라면 성능이 극적으로 개선된다. cilk_spawn은 뒤에 호출하는 함수를 병렬로 처리하면서 이후 작업을 계속 하도록 한다. 그리고 이렇게 펼쳐진 작업들은cilk_sync에서 만나게 된다. 즉, 첫 네 개의 연산은 각각 병렬로 작업을 세 개 시작하고 마지막은 현재 프로세스가 직접 처리한다. 그 후 첫번째cilk_sync에서 모든 작업이 만나 동기화된다. 이후 뒤 네 개의 작업도 마찬가지로 동작한다. 이를 통해서C += A * B연산을 위의 수식에 따라 8개의 곱셈과 하나의 덧셈으로 처리할 수 있다.
그러면 기저 조건의 임계 크기가 얼마가 되어야 최적의 성능을 얻을 수 있을까? 이 역시 실험으로 찾아내야 하는 파라미터 값이다. 당연하지만 여기서 작업을 이전의 절반으로 나누고 있으므로 이 기저 조건 값은 2의 배수여야 잘 동작 한다.
| 기저 조건 크기 (Threshold) | 실행 시간 (초) |
|---|---|
| 4 | 3.00 |
| 8 | 1.34 |
| 16 | 1.34 |
| 32 | 1.30 |
| 64 | 1.95 |
| 128 | 2.08 |
32가 최적의 값이다. 이게 왜 최적의 값일까? 기저 조건이 32라는 뜻은, 문제를 쪼개어서 32x32 크기의 타일이 한번에 풀어야 하는 최소 행렬의 크기라는 뜻이다. 위의 코드에서 \(C += A \times B\) 를 계산하므로 A, B, C 총 세 개의 행렬(타일)이 모두 캐시에 올라가면 아주 빠를 것이다. 이걸 바탕으로 계산해보면 32 $\times$ 32 $\times$ 8 (double의 크기) $\times$ 3 = 24KB로, L1 캐시에 딱 넘치지 않고 올라간다는 것을 알 수 있다. 만약 크기가 64였다면 96KB로 L2 캐시엔 들어가지만 L1은 넘친다. L1, L2 모두 넘치지 않으면서 가장 큰 크기의 타일링을 처리할 때 가장 빠른 실행 시간을 보인 것이다. 그리고 L1, L2 캐시는 각각 코어 전용으로 달려있기 때문에, cilk_spawn을 통해서 재귀적으로 분할된 문제들을 풀 때 모든 18개의 코어가 각자에 독점적으로 달려있는 L1, L2 캐시에 기저 조건으로 풀어야 하는 문제의 모든 행렬 데이터가 담겨 있기 때문에 가장 빠른 성능을 낸 것이다.
아무튼 또 한번의 극적인 최적화가 이루어 져서 기존 대비 36%의 성능을 개선하여 최대 성능의 12.65%를 달성했다. 근데 정말로 계산한 대로 캐시를 더 활용한 걸까? 이 역시 캐시 프로파일링을 살펴보면 알 수 있다.
| 버전 | 캐시 레퍼런스 (백만) | L1 데이터 캐시 미스 (백만) | LLC 미스 (백만) |
|---|---|---|---|
| 버전 6 (병렬 처리 ) | 104,090 | 17,220 | 8,600 |
| 버전 7 (타일링) | 64,690 | 11,777 | 416 |
| 버전 8 (병렬로 분할 정복) | 58,230 | 9,407 | 64 |
LLC 기준 캐시 미스율이 약 85% 개선되었다.
버전 9: Vectorization
아직 끝난게 아니다.
우리의 실험 머신 스펙을 다시 살펴보자. 처음에 이론적인 Peak GFLOPS를 잴 때 여러가지를 고려했는데 그 중 하나가 바로 AVX, 즉 하드웨어 자체에서 제공하는 벡터화 (Vectorization) 를 활용하는 것이었다. 그래서 우리는 하나의 FPU가 최대 8배의 연산을 처리할 수 있다고 가정할 수 있었다. 지금까지 우리의 최적화는 대부분 캐시나 메모리와 관련된 것들이 많았기 때문에, 이제는 특정 하드웨어에서만 가능한 최적화에 기대볼 수 있다.
현대 프로세서에 탑재된 벡터 하드웨어는 데이터를 SIMD (Single Instruction Stream, Multiple Data Stream) 방식으로 처리할 수 있다. 256 비트 크기의 레인인 벡터 레지스터라는 것이 따로 탑재되어 있어서, 같은 연산을 서로 다른 데이터에다가 적용할 때 이 크기만큼 한번에 처리할 수 있게 해준다. 실제로는 코드를 직접 수정하지 않아도 우리보다 똑똑한 컴파일러가 -O2 레벨 이상의 최적화 옵션에서 이걸 알아서 해주기도 한다. 컴파일러가 어느 부분을 벡터화했는지 알고 싶으면 -Rpass=vector 옵션을 줘서 벡터화 관련 리포트를 받아볼 수 있다.
clang -O3 -std=c99 mm.c -o mm -Rpass=vector
mm.c:42:7: remark: vectorized loop (vectorization width: 2, interleaved count: 2) [-Rpass=loop-vectorize]
for (int j = 0; j < n; j++)
^
하지만, 대부분의 머신에서 최신 벡터 연산을 지원하지는 않기 때문에, 컴파일러는 기본적으로 아주 보수적인 연산만을 적용한다. 그래서 컴파일 시에 추가적인 플래그를 통해서 구체적으로 어떤 연산을 적용할지를 알려줄 수 있다.
-mavx: 인텔의 AVX 벡터 연산 사용-mavx2: 인텔의 AVX2 벡터 연산 사용-mfma: FMA 연산 사용-march=<string>:<string>으로 명세한 아키텍쳐에서 사용 가능한 연산이면 뭐든지 사용-march=native: 해당 아키텍쳐에서 컴파일할 때 사용 가능한 연산이면 뭐든지 사용
참고로 부동 소수점 연산의 제약으로 인해서, 이런 벡터화 플래그를 켤 때에는 -ffast-math 같은 다른 추가적인 플래그가 필요할 수도 있다.
아무튼, 버전 9까지 최적화한 코드에 -march=native -ffast-math 옵션을 주면 또 한번 극적으로 성능이 두 배 가량 증가해서 0.7초, Peak GFLOPS의 23.48%를 달성한다.
버전 10: AVX Intrinsics
인텔은 AVX 하드웨어 벡터 연산을 엔지니어가 직접 다룰 수 있도록 하는 C 스타일의 API를 제공하는데 이를 AVX Intrinsic Instructions라고 한다. 버전 9까지 얹은 최적화에다가 계속해서 다음과 같은 것들을 적용하고, 측정하고, 개선하고, 실험하는 등 성능을 엔지니어링할 수 있다.
- 데이터 전처리: 곱셈을 수행하기 전에 데이터를 미리 정규화하거나, 차원을 축소하거나, 메모리 레이아웃을 최적화 해볼 수 있다.
- 행렬 전치 연산: 별 생각없이 구현하면, 행렬은 행 우선 (row-major) 순서로 메모리에 저장된다. 그러면 행렬의 곱셈 \(C = A \times B\)에서, 뒤에 곱해지는 행렬 B는 열 우선 (column-major) 순서로 접근하게 되므로 공간 지역성이 깨진다. 그래서 B를 미리 전치(Transpose)한 다음 곱할 때 접근 순서를 잘 고려하면 각 행을 순차적으로 접근할 수 있다.
- 데이터 정렬 (Alignment): 앞에서 적용한 타일링을 최대한 적용할 수 있도록 행렬 내부를 블록 단위로 재배치 해볼 수 있다.
- 메모리 관리 최적화: 행렬 크기가 커지면 계산에 필요한 메모리 양도 많아지는데, 이를 효율적으로 처리하기 위해서 메모리 풀, 제자리 연산, 메모리를 페이지 경계에 정렬하기 등을 고려해볼 수 있다.
- AVX Intrinsics를 적용해서 기저 조건 함수 개선: 기저 조건인
mm_base에서 단순한 반복문을 쓰는게 아니라 직접 AVX Intrinsics를 명시적으로 사용할 수 있다.
특히, 버전 9에서 -Rpass=vector 레포트 결과를 보면 벡터화의 크기(width)가 2 밖에 안되었다. 하지만 우리는 직접 AVX Intrinsics을 이용해서 256 비트의 벡터, 즉 4개의 배정밀도 부동 소수점 연산을 다음과 같이 한번에 처리할 수 있다. (참고로 아래 코드는 n이 4의 배수일 때를 가정한 코드이다)
#include <immintrin.h>
void mm_base(
double *restrict C, int n_C,
double *restrict A, int n_A,
double *restrict B, int n_B,
int n) {
for (int i = 0; i < n; i++) {
for (int k = 0; k < n; k++) {
// A[i][k]를 브로드캐스트할 벡터 준비.
// 스칼라 값을 벡터 레지스터 4개 레인에 브로드캐스트 한다.
__m256d a_vec = _mm256_set1_pd(A[n_A * i + k]);
for (int j = 0; j < n; j += 4) {
// B의 원소 4개 연속 로드.
// 정렬되지 않은 메모리에서, 4개의 배정밀도 부동 소수점으로 로드한다.
__m256d b_vec = _mm256_loadu_pd(&B[n_B * k + j]);
// C의 원소 4개 연속 로드. 마찬가지.
__m256d c_vec = _mm256_loadu_pd(&C[n_C * i + j]);
// FMA 시도 - c_vec += (a_vec * b_vec)
c_vec = _mm256_fmadd_pd(a_vec, b_vec, c_vec);
// 결과 저장. 4개의 배정밀도 부동 소수점을 동시에 저장한다.
_mm256_storeu_pd(&C[n_C * i + j], c_vec);
}
}
}
}
위의 항목 중에서 정확히 어떤 걸 적용해서 실험했는지는 슬라이드에 나와있지 않지만 (아마도 마지막 항목은 적용했을 거라고 생각됨), 이것들을 다 개선하면 또 한번의 큰 폭의 성능 개선을 얻어서 최종적으로는 0.39초, 최대 성능의 약 42.15%에 도달할 수 있다.
버전 11: 인더스트리 라이브러리
사실 여기까지 노력했던 모든 최적화들은 인더스트리에서 쓰이는 행렬 라이브러리에 다 녹아 있다. 예를 들어, 인텔의 MKL (Math Kernel Library)에는 이 모든 최적화들이 다 적용되어 있다.
#include <stdio.h>
#include <stdlib.h>
#include "mkl.h"
#define SIZE_MATRIX 4096
#define SIZE_TILING 32
int main() {
double *A, *B, *C;
// 64-byte alignment
A = (double *) mkl_malloc(SIZE_MATRIX * SIZE_MATRIX * sizeof(double), 64);
B = (double *) mkl_malloc(SIZE_MATRIX * SIZE_MATRIX * sizeof(double), 64);
C = (double *) mkl_malloc(SIZE_MATRIX * SIZE_MATRIX * sizeof(double), 64);
//
// initialise matrices with randome values...
//
for (int tj = 0; tj < SIZE_MATRIX; tj += SIZE_TILING) {
for (int ti = 0; ti < SIZE_MATRIX; ti += SIZE_TILING) {
for (tk = 0; tk < k; tk += SIZE_TILING) {
int tile_m = (ti + SIZE_TILING > SIZE_MATRIX) ? (SIZE_MATRIX - ti) : SIZE_TILING;
int tile_n = (tj + SIZE_TILING > SIZE_MATRIX) ? (SIZE_MATRIX - tj) : SIZE_TILING;
int tile_k = (tk + SIZE_TILING > SIZE_MATRIX) ? (SIZE_MATRIX - tk) : SIZE_TILING;
// 첫번째 반복일때만 0, 이후는 누적(1.0)
double beta_vec = (tk == 0) ? 0.0 : 1.0;
cblas_dgemm(
CblasRowMajor,
CblasNoTrans,
CblasNoTrans,
tile_m,
tile_n,
tile_k,
alpha,
B + ti * k + tk, // B의 타일 시작 위치
SIZE_MATRIX, // B의 leading dimension
A + tk * SIZE_MATRIX + tj, // A의 타일 시작 위치
SIZE_MATRIX, // A의 leading dimension
beta_vec,
C + ti * SIZE_MATRIX + tj, // C의 타일 시작 위치
SIZE_MATRIX); // C의 leading dimension
}
}
}
mkl_free(A);
mkl_free(B);
mkl_free(C);
return 0;
}
이 코드는 0.41초, 최대 성능의 40.10%를 보여준다. 우리가 열심히 최적화를 쌓아 온 버전 10과 비교했을 때 오차 범위 이내의 성능을 보여준다.
정리 및 최종 결론
최종적으로 이때까지 진행한 모든 최적화들과 성능들을 한 표로 정리하면 다음과 같다.
| 버전 | 구현 방법 | 실행 시간 (초) | 최대 성능 대비 몇 %? | 물리적인 최대 성능만 고려 시 몇 %? |
|---|---|---|---|---|
| 1 | 파이썬 | 21,042 | 0.00078% | 0.00156% |
| 2 | 자바 | 2,738 | 0.006% | 0.012% |
| 3 | C | 1,156 | 0.014% | 0.028% |
| 4 | + 반복문 중첩 순서 바꾸기 | 177.68 | 0.093% | 0.186% |
| 5 | + 컴파일러 최적화 | 54.63 | 0.30% | 0.60% |
| 6 | 병렬 처리 | 3.18 | 5.17% | 10.34% |
| 7 | + 고정 크기 타일링 | 1.74 | 9.45% | 18.9% |
| 8 | 병렬로 분할정복 | 1.30 | 12.65% | 25.30% |
| 9 | + 컴파일러 최적화 (Vectorization) | 0.7 | 23.48% | 46.96% |
| 10 | + AVX Intrinsics | 0.39 | 42.15% | 84.30% |
| 11 | Intel MKL | 0.41 | 40.10% | 80.20% |
아주 간단하지만 굉장히 느렸던 버전 1의 파이썬 구현부터, 하드웨어 및 소프트웨어가 어떻게 동작하는지를 이해하고 행렬 곱셈 문제 자체의 특징을 고려하여 다양한 아이디어를 직접 구현하고, 관련된 파라미터를 튜닝하고, 실험하고, 측정하고, 이런 이터레이션을 반복하면서 점진적으로 개선한 끝에 버전 10에 와서는 인더스트리 라이브러리에 맞먹는 성능을 낼 수 있었다. 당장 6시간 걸리던 연산이 0.4초만에 끝난다고 상상해보면 정말 엄청난 개선이다. 심지어, 앞에서 최대 성능을 계산할 때 2-way 하이퍼스레딩을 고려해야 하는지에 대해서 개인적인 의문이 있었는데, 만약 이걸 고려하지 않는다면, 표의 마지막 컬럼에서 보듯이 성능 엔지니어링을 통해 물리적인 머신의 최대 성능의 84.30%를 뽑아내었다.
물론 이정도의 극적인 성능 개선은 좀처럼 찾아보기 힘들다고 한다. 그만큼 행렬 곱셈이 많이 연구된 분야이면서, 또 이런 다양한 최적화를 적용해볼 수 있는 좋은 문제라는 생각이 든다. 여기서 적용한 다양한 엔지니어링 방법들을 다른 문제에 적용해볼 수 있는 기회가 있으면 좋겠다.
-
캐시 성능을 측정하는 게 아니라 시뮬레이션하는 이유는 현대 하드웨어와 그 실행 환경의 복잡성으로 인한 한계 때문이다. 실제 CPU의 성능 카운터로는 모든 캐시 동작을 정확하게 기록할 수 없다. 그리고 프로그램이 실행되는 환경, 예를 들어 prefetch나 speculation 같은 하드웨어 측면의 간섭과, OS의 스케쥴링, 백그라운드 프로세스 등 소프트웨어 측면의 간섭으로 인해서 정확한 측정이 불가능하다. 그래서 Cachegrind는 프로그램을 직접 실행하긴 하면서 가상의 캐시 모델을 기반으로 캐시 동작을 시뮬레이션 한다. 프로그램의 모든 메모리 접근을 추적하고, 이게 진짜 캐시에 어떻게 반영될지를 계산하는 것이다. ↩
-
참고로, Cachegrind는 디폴트로 L1, L2, L3의 여러 개의 캐시 중 LL (Last Level)을 중심으로 캐시 미스율을 계산한다. 실제로는 L1, L2, L3를 모두 시뮬레이션 하지만, CPU와 메인 메모리 사이의 마지막 관문이 바로 이 LLC라서 이걸 넘어가는 순간 성능 저하가 매우 크기 때문에 가장 중요한 지표라고 볼 수 있다. ↩