/home/caml-shaving

Soundness

정적 분석과 안전함

2018-08-20

태그: dev think

이 글은 Michel Hicks의 “What is soundness in static analysis?”에 대한 리뷰이다. 수학적 증명과 정적 분석에서의 Soundness, Completeness는 그 뿌리는 같지만 미묘하게 다르다. 이 글은 두 가지 분야에서의 Soundness, Completeness, Soundiness, 그리고 정적 분석에서 많이 사용되는 용어인 Precision, Recall 등을 설명하고 소개하는 글이다. 이런 용어에 대한 이해는 정적 분석을 평가하기 위한 좋은 벤치마크 도구가 된다.

정적 분석에서의 ‘안전함’(Soundness)

‘안전함’이라는 용어는 수학의 형식 논리에서 왔다. 여기에는 증명 체계와 모델이라는 개념이 있다. 증명 체계는 모델에 대한 성질(또는 statement)을 증명할 수 있는 규칙의 집합이다. 이건 마치 어떤 도메인 위에서 정의된 집합처럼 수학적인 구조이다. 증명 체계 L이 증명할 수 있는 어떤 성질이 그 모델 위에서 정말로 참이 된다면, 우리는 그런 증명 체계를 안전(sound)하다고 한다. 반면 모델 위에서 참인 모든 성질을 증명할 수 있다면, 그런 층명 체계를 완전(complete)하다고 한다. 사실 괴델의 불완전성 정리에 의해서 어떤 증명 체계도 안전한 동시에 완전할 수 없다. 즉, 참이지만 L이 증명할 수 없는 어떤 성질이 항상 있거나, 아니면 L이 (다른 모든 참인 성질과 더불어) 어떤 거짓 성질을 참이라고 잘못 증명해버릴 수도 있다.

그럼 이제 정적 분석을 ‘모든 프로그램 실행에 적용되는 어떤 성질이 있는지 대한 증명 체계’로 볼 수 있다. 프로그램(즉, 가능한 실행)이 모델의 역할을 한다. 예를 들어, 정적 분석기 Sparrow는, ‘어떤 프로그램 실행도 버퍼 오버 플로우 등으로 인한 런타임 에러를 보이지 않는다’는 성질 R을 증명하는 것을 목표로 한다. 만약, Sparrow가 어떤 프로그램에 대해 성질 R이 만족한다고 말하고, 정말로 그 프로그램의 어떤 실행 흐름도 런타임 에러가 없다면(즉 성질 R을 만족한다면), Sparrow는 안전(Sound)하다고 간주된다. 반면 R을 만족하지 않는데 만족한다고 말하면, 이건 불안전(Unsound)한 것이다. 즉, 적어도 하나의 실행이 런타임 에러를 갖는데 ‘런타임 에러가 없다’고 말하면 그렇다는 거다.

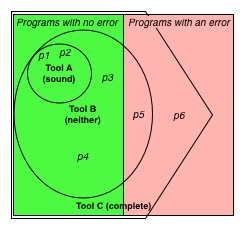
sound-complete

위 그림은 이런 상황을 보여준다. 왼쪽 절반(녹색)은 성질 R을 만족하는 모든 프로그램을 나타낸다. 즉, 여기 속한 애들은 절대 런타임 에러가 없다. 오른쪽 절반은 반대로 성질 R을 만족하지 못하는, 즉 어떤 실행 흐름이 런타임 에러를 뱉는 모든 프로그램을 나타낸다.

왼쪽 위의 제일 작은 동그라미(Tool A(Sound)) 안에 있는 프로그램 p1, p2는 분석기 A가 성질 R을 만족한다고 말하는 것들이다. 이 동그라미 밖에 있는 모든 프로그램들(p3-p6)은 A에 의해 증명되지 않는다. 이 동그라미가 정확히 왼쪽 절반에만 있기 때문에, A는 안전하다: 즉, A는 에러가 있는 프로그램에 대해 ‘에러가 없다’고 절대 말하지 않는다.

다시 말하면, 위 그림에서 각 도형(동그라미, 오각형)은 분석기가 참이라고 증명하는 프로그램의 범위를 나타낸다. 즉, 도형 안에 있는 프로그램에 대해서는 아무런 알람을 내지 않는다(= 성질 R, 즉 ‘런타임 에러가 없다’는 사실을 증명한다). 반면에 도형 바깥에 있는 프로그램에 대해서는 ‘런타임 에러가 있다’고 알람을 내는 것이다. 예를 들자면 분석기 A는 p1, p2에 대해서는 아무런 알람을 내지 않는다. 이것은 참이다. 하지만 p3, p4에 대해서는 알람을 내어버린다. 이것은 거짓이다. p5, p6에 대해서도 역시 알람을 낸다. p5, p6은 실제로 런타임 에러가 있기 때문에 이것은 사실이다. 즉, 분석기 A는 에러가 있는 프로그램(p5, p6)에 대해서 반드시 알람을 내기 때문에 안전한 것이다.

또한 앞서 말했듯이 괴델의 불완전성 정리에 의해 분석기 역시 안전하면서 완전할 수 없으므로, 세상의 그 어떤 분석기도 그림의 딱 왼쪽 절반(오른쪽, 즉 p1-p4)만을 정확히 커버할 순 없다. 모든 분석기는 왼쪽 절반보다 작은 부분 집합만을 커버하거나, 아니면 왼쪽 절반을 포함하면서 동시에 오른쪽 절반의 일부도 반드시 포함할 수 밖에 없는 것이다.

‘거짓 알람’(False Alarms)과 ‘완전함’(Completeness)

정적 분석은 일반적으로 어떤 프로그램 P를 분석할 때, R과 같은 성질에 대한 알람을 전혀 내지 않음으로써 이 성질을 만족한다고 분석한다. 그러므로 위의 예시에서, 분석기 A는 p1과 p2에 대해 어떤 알람도 내지 않는다. 대신 동그라미 바깥에 있는 다른 프로그램을 분석할 때는 어떤 알람을 낼 것이다. 따라서 동그라미 바깥에 있으면서 왼쪽 절반에 있는 p3, p4 같은 프로그램을 분석기 A가 분석하면 알람을 내게 되는데, 이를 거짓 알람(false alarm)이라고 한다. 실제로는 런타임 에러가 없지만, 분석기 A는 런타임 에러가 난다고 알람을 띄우기 때문에.

거짓 알람은 어쩔 수 없는 현실이다. 그래서 도구 사용자들이 좌절한다. 대부분의 개발자는 분석기를 (어느 정도) 불안전하게 만들면서 거짓 알람을 줄이려고 한다. 예를 들어 위의 그림에서, 분석기 B(neither)는 불안전하다: B의 동그라미에는 p5와 같이 오른쪽 절반에 있는 프로그램도 들어있기 때문이다.

극단적으로, 분석기는 알람이 참일 때만 알림을 낼 수도 있다. 예를 들어 심볼릭 실행기 KLEE가 있는데, KLEE가 찾아내는 각각의 알람은 실제로 런타임 에러를 일으키는 입력까지 찾아준다. 이렇게 알람이 절대 거짓이 아닌 분석기를 완전(Complete)하다고 한다. 증명 이론으로 돌아가서 보면, 분석기가 알람을 안내면 대상 프로그램이 분석 성질을 만족하는 것이다. 그러므로, 완전한 분석기는 유효한(성질을 만족하는) 프로그램에 대해 절대 알람을 내면 안된다. 즉, (놓치는 에러가 있더라도) 거짓 알람이 없어야 한다.

다시 그림으로 돌아가보면, 분석기 C(complete)는 완전하다: 그림의 오각형이 왼쪽 절반을 완전히 담고 있지만, 오른쪽 절반도 담고 있다. 즉, 분석기 C는 모든 올바른 프로그램에 대해서 성질 R을 증명할테지만, 런타임 에러가 있는 어떤 프로그램들에 대해서도 (알람을 내지 않음으로써) 역시 성질 R을 증명해버린다

Soundiness

안전과 완전이라는 용어에 대한 문제는 그 자체로 많은 것을 뜻하지는 않는다는 점이다. 모든 프로그램에 대해서 알람을 내는 분석기는 평범하게 안전하다. 모든 프로그램을 (알람을 내지 않음으로써) 허락해버리는 분석기는 평범하게 완전하다. 이상적으로 분석기는 안전함과 완전함 모두를 추구해야 한다. 비록 완벽하게 불가능하지만 말이다. 그럼 어떤 분석기가 얼마나 그것(안전함+완전함)에 근접한지는 어떻게 알까? 이분법적으로 안전함/완전함을 가르는 것은 아무것도 말해주지 않는다.

이 문제를 해결하기 위한 방법 중 하나의 제안이 바로 soundiness이다. Soundy한 분석기는 특정 프로그래밍 패턴이나 프로그래밍 언어의 특정 성질을 올바르게 분석하지 않는 대신, 이런 성질을 사용하지 않는 프로그램에 대해서는 안전하다(그리고 거짓 알람도 적게 낸다). 예를 들어, 많은 자바 분석기는 soundy한데, reflection이라는 언어의 성질을 무시하도록 하면서 이걸 가능케 했다. 왜냐하면 reflection을 제대로 다룰려면 엄청나게 많은 거짓 알람과 성능 문제를 일으키기 때문이다.

Soundiness에 대한 이런 아이디어는 매력적인데, 안전함을 목표로 하는 분석기를, 단순히 불안전하다고 취급하면서 다른 훨씬 정교하지 못한 분석기와 나란히 취급하는 게 아니라, 제대로 가려낼 수 있기 때문이다. 그런데 몇몇은 이 soundiness의 아이디어를 별 의미가 없다고 까기도 한다. 근본적으로 “어떤 가정치까지는 안전”함을 뜻하기 때문이다. 하지만, 모든 도구(분석기)는 저마다의 가정을 한다. 그러므로 soundy한 두 분석기의 결과는 (거의) 비교 불가능하다. 반면에, sound한 두 분석기의 결과는 비교할 수 있다는 것이다.

그저 분석기가 soundy하다고 말하기 보다는, 어떤 가정치까지는 안전하다고 말해야 한다. 그리고 그런 가정을 나열해야 한다. 예를 들어, Astree 분석기의 경우, 분석할 프로그램이 동적 메모리 할당을 하지 않는다면(가정), 안전하다.

Precision과 Recall

절대적으로 안점함을 증명하는 게 아니라 ‘어떤 가정까지 안전함’을 증명하는 것 자체로는 여전히 많은 걸 말해주진 않는다. 어쨌든 분석기(도구)의 유용함을 판단할 방법이 필요하다. 분석기는 약간의 나쁜 프로그램을 제외한 대부분의 좋은 프로그램을 가려낼 줄 알아야 하고, 아주 최소한의 거짓 알람을 내야 한다. 이런 분석기의 유용함을 알려주는 계량적인 방법 중 하나가 바로 Precision과 Call이다. 전자는 분석기가 주장한 알람이 얼마나 맞는지를 알려주고, 후자는 알람이 맞을 가능성에 대한 비율을 측정한다.

구체적인 정의는 다음과 같다. 프로그램 N개를 분석한다고 하자. 이때,

그러면, 이 분석기의 Precision은 \(\frac{T}{T+F}\)가 되고 Recall은 \(\frac{T}{X}\)가 된다. (이때 \(T\)와 \(F\)가 각각 True Alarm, False Alarm이 아니라는 것에 주의할 필요가 있다)

안전한 분석은 \(F=0\)일 것이므로 100%의 Precision을 가질 것이다. 완전한 분석은 \(T=X\)일 것이므로 완벽한 Recall(\(=1\))을 가질 것이다. 실용적인 분석은 이 근처 어딘가에 있을 것이다. 이상적인 경우는 Precision과 Recall 둘다 1에 근접하게 만드는 것이다.

앞서 그림을 다시 보자. 세 가지 분석기(=도형)와 프로그램 p1-p6에 대해서 Precision과 Recall을 계산해보자. 일단 \(N=6\)이고 \(X=4\)다. 분석기 A 에 대해서 \(T=2\)이고 \(F=0\)이므로 \(Precision = 1\)이고 \(Recall = \frac{1}{2}\)가 된다. 분석기 B는 \(T=4\)이고 \(F=1\)이므로 \(Precision = \frac{4}{5}\)이고 \(Recall = 1\)이 된다. 마지막으로 분석기 C는 \(T=4, F=2\)이고 \(Precision=\frac{2}{3}, Recall=1\)이 된다.

한계점

Precision과 Recall이 안전함과 완전함에 대한 실용성의 구멍을 어느 정도는 메꿔주지만, 문제점이 없는 건 아니다. 그 중 하나는 이런 측정 방법이 본질적으로 경험적이라는 것이다. 잘 해 봤자 어떤 프로그램에 대해서만 Precision/Recall을 계산할 수 있을 뿐이다. 즉, (p1-p6과 같은) 벤치마크 모음에 대해서만 계산해놓고, 이런 수치가 모든 다른 프로그램에 대해 맞길 바랄 뿐이다. 또 다른 문제점은 프로그램이 언제 그런 성질을 만족하는지, 만족하지 않는지 알기가 매우 어렵다는 점이다. 즉, 애초에 기저에 깔린 믿음이 부족할 수도 있다.

또 다른 문제점은 Precision과 Recall을 모든 프로그램에 대해 정의한 것이다. 하지만, 실제 프로그램은 충분히 크고 복잡해서 아주 잘 엔지니어링한 분석기도 거짓 알람을 내어서 대부분을 잘못 분석할 수도 있다. 그런 경우, 전체 프로그램에 집중하기 보다는, 프로그램의 특정 버그에만 집중하도록 할 수 있다. 예를 들어, 버퍼 오버플로우 성질을 증명하기 위한 도구에 대해서는, 먼저 버퍼에 접근하는 모든 표현식의 수를 세고(\(N\)), 안전하게 버퍼에 접근한 표현식의 수를 센 다음(\(X\)), 분석기가 올바르게 알람을 내지 않음으로써 증명한 수(\(T\))와 알람을 내는데 실패해서 틀리게 증명한 수(\(F\))를 세면 된다. Astree 같은 경우는 이렇게 하면 아주 잘 맞는다. 125,000 줄의 프로그램에 대해서 고작 3개의 거짓 알람만을 낸다고 한다.

이런 정의는 여전히 기저에 깔린 믿음, 즉 굉장히 알기 어려운 \(X\)를 알아야 하는 문제점이 있다. 예를 들어, Data race 버그 같은 경우는 \(X\)를 알아내기가 굉장히 어렵다. 또, 잠재적인 버그의 수를 세기도 힘들다. 예를 들어, Data race 같은 경우, 데이터를 읽고 쓰는 모든 가능한 스레드/프로그램 포인트의 조합을 고려해야 하는데, 이건 말도 안된다. 버그 수를 세는 방법의 문제점은 “대체 버그가 뭐냐?”라는 철학적인 질문에 맞닿아 있다. 버그와 버그 아닌 것을 어떻게 구분할 것인가?

결론

안전함과 완전함은 분석기의 유효성에 대한 경계를 말해준다. 완벽한 분석기는 둘 다 만족하겠지. 하지만 완벽은 보통 불가능하고, 그냥 안전하던가 완전하던가 둘 중 하나만 하는 것은 현실에서는 별로 도움되지 않는다. Precision과 Recall은 수치를 제공하긴 하는데, 특정 벤치마크 모음에 관해서, 뭐가 버그인지 정확히 구분되는 경우에만 계산될 뿐이다. 대부분의 경우, 벤치마크 모음이 얼마나 보편적인지는 증명되지 않고, 뭐가 버그인지도 정확히 모른다.

가령, 정적 분석을 평가하기 위한 가장 효과적인 접근은 모든 프로그램에 대해서는 (일정 가정까지는) 안전하거나 완전하고, 동시에 어떤 프로그램들에 대해서는 부정확하지만 수치를 제공하는 것일 수 있다. 두 종류의 주장 모두 유효성과 보편성에 대한 증거를 준다.

이걸 잘 하려면, 보편성과 (적어도 어느 정도는)믿음직한 독립적인 증거를 뒷받침해주는 벤치마크 모음이 필요하다. (저자의) 개인적인 인상으로는, 정적 분석 문제들에 대해서는 진짜 별로 좋은 선택이 없다. 부디 이 글이 이런 문제를 잘 알리길 바라고 추후의 많은 연구를 기대해 본다.