Introduction

OCaml을 가지고 백준에서 PS를 하는 팁을 설명해둔 책이다.

Standard Library

글을 쓰고 있는 2023년 하반기 기준으로 백준의 언어 정보탭을 보면 OCaml 4.11.1 버전을 사용하고 있음을 확인할 수 있다. OCaml 4.11.1 버전의 표준 라이브러리 문서를 보면서 PS에 필요한 사용법을 익히자.

단, 애플 실리콘 맥의 경우 4.11.1 버전이 없다. 아쉬운대로 4.12.1를 쓰자.

Reading Inputs

Integer Input

정수를 입력받는 방법은 크게 두 가지가 있다.

참고로 OCaml의 기본 int 타입은 32비트도 64비트도 아닌 63비트로 -461경에서 461경 사이의 값을 표현할 수 있다. 정말 64비트, -922경~922경 정도의 범위가 필요한 문제가 아니라면 웬만해서는 내장 int 타입으로 다 커버 가능하다.

`read_int`

먼저 표준 입력에 대한 입력 함수를 사용하는 방법이다.

val read_int : unit -> int

가장 쉬운 방법은 read_int를 쓰는 거다. OCaml 정수 (즉, 63비트) 하나를 읽어들인다. 하지만 구체적인 포매팅을 못하기 때문에 입력이 많거나 복잡한 문제에서 썼다가는 런타임 에러를 만날 확률이 높아진다. 입력이 1~2개로 끝나는 경우에 주로 쓴다.

`Scanf.scanf`

사실 OCaml은 그 자체로 C 런타임¹이므로 C에서 쓰이는 방법들을 모두 사용할 수 있다. 그 중에서도 C의 scanf를 바인딩해둔 Scanf.scanf를 쓰면 된다.

let input = Scanf.scanf "%d " (fun x -> x) ;;

아래 코드와 의미적으로 동일하다:

int x;
scanf("%d ", &x);

입력 여러 개를 한 번에 받을 수도 있다.

let a, b = Scanf.scanf "%d %d" (fun x y -> x y);;

포맷 스트링의 개수만큼 함수 인자가 늘어난다고 생각하면 된다. OCaml의 Scanf.scanf 타입은 엉망진창이기 때문에 이해하려고 시도하지 않는게 좋다.

String Input

문자열 입력도 비슷하다.

`read_line`

val read_line : unit -> string

뉴라인을 만날 때까지 입력 한 줄을 통째로 받는다. 공백도 포함한다. 마지막 뉴라인 문자는 알아서 잘라준다.

보통 입력을 이렇게 한 줄 받으면 공백이나 컴마를 기준으로 자르는 등의 후처리가 필요한 경우가 많다. 이럴땐 다음 함수를 쓰면 된다.

val String.split_on_char : char -> string -> stirng list

즉, String.split_on_char sep (read_line ()) 하면 한 줄을 읽어들인 다음 sep을 기준으로 문자열을 잘라서 문자열 리스트로 돌려준다. 문자열이나 트리 관련 문제에서 쓰인다.

`Scanf.scanf`

read_line은 아래 코드와 완전히 동일하다.

Scanf.scanf "%[^\n]"

[ ]안의 정규식으로 입력을 지정할 수 있고 여기에 ^\n를 해줘서 뉴라인 빼고 전부 다 읽어들이게 하면 된다. 단, 정규식 엔진을 돌려야 하기 때문에 read_line 보다는 느리다.

그래서 성능도 꽤 좋은편이다; 실제로 백준의 언어 탭에 가보면 자바나 파이썬처럼 채점 시 시간 제한은 없고 메모리만 32MB 더 얹어준다.

Output

`print_xxx` 계열

val print_char : char -> unit

val print_string : string -> unit

val print_bytes : bytes -> unit

val print_int : int -> unit

val print_float : float -> unit

위의 함수들을 타입에 맞게 적절히 사용하면 된다

단, 아래 두 함수는 주의해야 한다.

val print_endline : string -> unit

val print_newline : unit -> unit

print_endline과 print_newline은 모두 뉴라인과 관련이 있는 출력 함수인데, 그것보다 중요한 것은 두 함수는 모두 문자열을 표준 출력에 뿌린 다음 표준 출력을 비운다(flush). 그래서 문제의 조건에 따라 엄청나게 많은 출력을 해야하는 경우 출력에 print_endline 을 쓰면 시간 초과가 뜬다.

반면에 위의 print_<primitive-type> 함수나, 아니면 아예 C 스타일의 Printf.printf "%..." 같은 포맷스트링 출력 함수의 경우 적절한 버퍼링을 관리하여 매번 표준 출력을 Flush하지 않기 때문에 출력이 많은 경우에 훨씬 더 효율적이다.

수 찾기 문제의 경우 핵심 알고리즘 자체는 정렬 후 이분탐색을 하거나 해시 테이블을 이용해서 검색을 빠르게 할 수 있다. 문제는 출력인데, 조건에 따라 M의 크기가 \( 1 \leq M \leq 100,000 \) 이라서 최대 10만번의 출력을 해야한다. 이 경우 각 줄의 답을 print_endline 으로 출력하면 시간 초과가 뜨고, print_string 을 이용하면 정답이 된다.

Linear Data Structures

구체적이고 합의된 정의가 있는 것은 아니지만, 대충 데이터 구조를 두 종류로 나눌 수 있는데 하나는 선형이고 다른 하나는 비선형이다. 선형 데이터 구조는 엘리먼트들을 (특히 메모리에서) 연속적으로(sequentially) 저장하여 관리하는데, 구현에 따라 다르겠지만 예를 들면 배열이나 스택, 큐, 링크드 리스트 같은 것들이 있다.

List

OCaml의 가장 기본적이며 가장 가볍게 자주 쓰이게 될 선형 데이터 구조 중 하나이다. 파이썬의 리스트(를 가장한 배열)과는 다르게 진짜로 링크드 리스트 구조이다. 대부분의 함수들이 재귀 함수로 구현되어 있는데, 그래서 꼬리 재귀가 아닌 함수들은 주의해서 호출해야 한다. 자칫 큰 리스트에 이런 함수를 호출하면 스택이 터질 수도 있다. 그래서 입력이 큰 경우는 꼬리 재귀 버전의 함수를 호출해야 해서 조금 비 직관적인 코드가 나올 수도 있다.

이름은 리스트이지만 그 동작은 스택과도 같다. 리스트의 헤드를 떼어 내는 작업이 O(1)이고, 리스트의 헤드에 원소를 추가하는 작업도 O(1)이기 때문에 이 성질을 활용할 수 있다. 반면에 리스트의 가장 마지막 원소를 가져오는 작업은 O(N)이며, 리스트의 가장 끝에 원소를 추가하는 작업은 직접 구현해야 하고 어떤 방법을 써도 O(N)이다.

기본 연산

val length : 'a list -> int

val compare_lengths : 'a list -> 'b list -> int

val compare_length_with : 'a list -> int -> int

val cons : 'a -> 'a list -> 'a list

val hd : 'a list -> 'a

val tl : 'a list -> 'a list

val nth : 'a list -> int -> 'a

val nth_opt : 'a list -> int -> 'a option

val rev : 'a list -> 'a list

val init : int -> (int -> 'a') -> 'a list

val append : 'a list -> 'a list -> 'a list

val rev_append : 'a list -> 'a list -> 'a list

val concat : 'a list list -> 'a list

val flatten = concat

대부분이 이름과 타입만 봐도 동작을 알 수 있다.

cons는 중위 연산자 ::이다.
List.init len f는 [f 0; f 1; ...; f (len-1)]과 같고 왼쪽에서부터 평가된다.
append는 중위 연산자 @이며, 꼬리 재귀가 아니다. 반면 rev_append는 List.rev l1 @ l2와 의미가 동일하지만 꼬리 재귀이며 따라서 더 효율적이다. 이로 인해서 두 리스트를 합칠 때는 첫 번째 리스트를 뒤집어서 rev_append를 하는 전략을 고민해봐야 한다.
concat과 flatten은 같은 동작을 하며, 꼬리 재귀가 아니다. 그래서 리스트의 리스트를 펴는 작업은 큰 입력이 예상될 때 되도록 하지 않는 것이 좋다.

Seq

Seq(시퀀스)는 OCaml의 특이한 데이터 구조 중 하나로, 지연 계산 리스트(delayed list) 이다. 즉, 다음 원소에 접근하려면 어떤 계산(평가)가 필요한 리스트이다. 이로 인해 무한한 시퀀스를 만들 수 있고, 순회하면서 시퀀스를 만들 수 있고, 미리 변환하지 않고 지연된 방식으로 시퀀스를 변환할 수 있다.

type 'a t = unit -> 'a node

'a 타입 원소를 담은 지연 계산 리스트의 타입이다. 구체화된 리스트의 노드 'a node는 lazy 블록이 아니라 클로져에 의해서 지연 계산되므로, 여기에 접근할 때마다 다시 계산될 수 있다.

type 'a node =
  | Nil
  | Cons of 'a * 'a t

계산 완료된 리스트의 노드로, 비어있거나 하나의 원소와 지연된 꼬리를 담고 있다.

기본 연산

val empty : 'a t

val return : 'a -> 'a t

val cons : 'a -> 'a t -> 'a t

val append : 'a t -> 'a t -> 'a t

val map : ('a -> 'b) -> 'a t -> 'b t

val filter : ('a -> bool) -> 'a t -> 'a t

val filter_map : ('a -> 'b option) -> 'a t -> 'b t

val fold_left : ('a -> 'b -> 'a) -> 'a -> 'b t -> 'a

val iter : ('a -> unit) -> 'a t -> unit

val unfold : ('b -> ('a * 'b) option) -> 'b -> 'a t

return을 제외한 나머지는 거진 다 리스트와 동일하다.

unfold가 좀 특이한데, 어떤 스텝 함수와 초기값으로부터 시퀀스를 만드는 함수이다. unfold f u를 호출하면, f u가 None이면 empty를 리턴하고, f u가 Some (x, y) 이면 Cons (x, unfold f y)를 리턴한다.

Array

Array 모듈의 함수를 살펴보자.

val make : init -> 'a -> 'a array

val create_float : int -> float array

val init : int -> (int -> 'a) -> 'a array

val make_matrix : int -> int -> 'a -> 'a array array

val length : 'a array -> int

val get : 'a array -> int -> 'a

val set : 'a array -> int -> 'a -> unit

val append : 'a array -> 'a array -> 'a array

val sub : 'a array -> int -> int -> 'a array

val blit : 'a array -> int -> 'a array -> int -> int -> unit

val sort : ('a -> 'a -> int) -> 'a array -> unit

val stable_sort : ('a -> 'a -> int) -> 'a array -> unit

val fast_sort : ('a -> 'a -> int) -> 'a array -> unit

생성

Array.make size x

모든 원소가 x인 size 크기의 배열을 만든다. 이때 모든 원소들은 x 와 물리적으로 같다. 즉 OCaml의 == 관계를 갖고, 이는 곧 같은 메모리를 가리킨다는 의미이다. 그래서 x에 가변 데이터를 넣으면 배열의 모든 원소가 같은 메모리를 가리키게 되므로 사이드 이펙트에 주의해야 한다.

Array.create_float size

size 크기의 실수 배열을 만든다. OCaml의 메모리 표현방식에 따라 무작정 실수를 배열에 담아버리면 모든 원소가 실수 값을 가리키는 굉장히 비효율적인 배열의 메모리 레이아웃이 나오므로, 실수 배열은 특별 취급해준다.

Array.init size (fun idx -> ...)

make랑 비슷한데 대신 idx에 따라 직접 원소의 초기값을 설정할 수 있게 해준다.

참고로 인덱스랑 같은 값을 갖는 정수 배열을 초기화할 때는 fun x -> x를 넘겨주기 보다는 다음과 같이 Fun 모듈의 id 함수를 쓰는게 좀더 효율적이다.

Array.init 5 Fun.id;;
(* create [|0; 1; 2; 3; 4;] *)

Array.make_matrix dim_x dim_y x

역시 create_float과 비슷한 이유로 2차원 배열 (행렬) 의 경우 효율적인 메모리 레이아웃을 고려하여 특별 취급해준다.

기본 연산

Array.get arr idx
(* equal to *)
arr.(idx)

랜덤 인덱스 접근 연산이다. 아래 표현은 신택스 슈거다.

Array.set arr idx x
(* equal to *)
arr.(idx) <- x

랜덤 인덱스 값을 업데이트하는 연산이다. 역시 아래 표현은 신택스 슈거다.

Stack

LIFO 스택으로, OCaml의 스택은 mutable list로 구현되어 제자리 수정(in-place modification)을 한다.

기본 연산

type 'a t

exception Empty

val create : unit -> 'a t

val push : 'a -> 'a t -> unit

val pop : 'a t -> 'a

val pop_opt : 'a t -> 'a option

val top : 'a t -> 'a

val top_opt : 'a t -> 'a option

val clear : 'a t -> unit

val copy : 'a t -> 'a t

val is_empty : 'a t -> bool

val length : 'a t -> int

val iter : ('a -> unit) -> 'a t -> unit

val fold : ('b -> 'a -> 'b) -> 'b -> 'a t -> 'b

기본 연산은 함수 이름을 보면 대충 알 수 있다. 스택은 가변 리스트로 구현되어 있기 때문에 create 을 통해서 만들어야 하고, 대입 연산은 얕은 복사만 하기 때문에 깊은 복사를 하려면 copy를 호출해야 한다.

이터레이터

val to_seq : 'a t -> 'a Seq.t

val add_seq : 'a t -> 'a Seq.t -> unit

val of_seq : 'a Seq.t -> 'a t

Queue

type 'a t

exception Empty

val create : unit -> 'a t

val add : 'a -> 'a t -> unit

val push : 'a -> 'a t -> unit

val take : 'a t -> 'a

val take_opt : 'a t -> 'a option

val pop : 'a t -> 'a

val peek : 'a t -> 'a

val peek_opt : 'a t -> 'a option

val top : 'a t -> 'a

val clear : 'a t -> unit

val copy : 'a t -> 'a t

val is_empty : 'a t -> bool

val length : 'a t -> int

val iter : ('a -> unit) -> 'a t -> unit

val fold : ('b -> 'a -> 'b) -> 'b -> 'a t -> 'b

val transfer : 'a t -> 'a t -> unit

val to_seq : 'a t -> 'a Seq.t

val add_seq : 'a t -> 'a Seq.t -> unit

val of_seq : 'a Seq.t -> 'a t

이름과 타입만 보면 대충 알 수 있다. 한 가지 문제점은 이게 단방향 큐라는 점이다. 문제에 따라서는 덱(Deque)이 필요할 수도 있는데, 그런 경우에는 직접 구현하는 수 밖에 없다.

가변 셀

덱을 구현하는 한 가지 방법은 일반적인 imperative에서 하는 것과 마찬가지로 두 개의 포인터와 사이즈 변수를 이용해서 링크드 리스트 기반의 환형 큐를 만드는 것이다. 이렇게 하면 원래의 Queue 모듈이랑 비슷하게 가변 데이터 구조를 구현한 것이다.

module Deque = struct
  exception Empty

  type 'a cell =
    | Nil
    | Cons of { content: 'a; mutable next: 'a cell }

  type 'a t = {
    mutable length: int ;
    mutable first: 'a cell ;
    mutable last: 'a cell
  }

  let create () = { length= 0; first= Nil; last= Nil }

  let clear q =
    q.length <- 0;
    q.first <- Nil;
    q.last <- Nil

  let add x q =
    let cell = Cons { content= x; next= Nil } in
    match q.last with
    | Nil ->
      q.length <- 1;
      q.first <- cell;
      q.last <- cell
    | Cons last ->
      q.length <- q.length + 1;
      last.next <- cell;
      q.last <- cell

  let push = add

  let head q =
    match q.first with
    | Nil -> raise Empty
    | Cons {content} -> content

  let take q =
    match q.first with
    | Nil -> raise Empty
    | Cons {content; next= Nil} ->
      clear q;
      content
    | Cons {content; next} ->
      q.length <- q.length - 1;
      q.first <- next;
      content

  let pop = take

  let tail q =
    match q.last with
    | Nil -> raise Empty
    | Cons {content} -> content

  let is_empty q = q.length = 0

  let length q = q.length
end

번외로 리스트(스택) 두 개를 이용해서 armotized 복잡도로 큐를 구현할 수도 있는데, 이 구현으로 덱을 구현하면 문제의 상황에 따라서 복잡도가 널뛸 수 있으므로 추천하지 않는다. (예를 들어, 아주 많은 원소를 집어넣은 다음 head, tail을 반복하면 리스트가 계속적으로 뒤집혀서 왔다갔다 해야하므로 O(N)의 복잡도가 꾸준히 소요되어서 armotization이 동작하지 않는다)

Non-linear Data Structures

Functor

OrderedType

Map

Set

HashedType

Hashtbl

Labels

Garbage Collection

OCaml은 Generational Hypothesis에 기반한 Generational Mark and Sweep Garbage Collection을 기반으로 메모리를 관리한다. 그래서 (특히 기본 정수의) 메모리 표현이 조금 특이한데 자세한 내용은 Memory Representation of Values와 Understanding the Garbage Collector를 참조하는 것이 가장 좋다. 여기서는 짧게 몇 가지만 언급하려고 한다.

힙의 종류

마이너 힙

가장 빠르다. 대부분의 메모리 블록은 제일 처음 마이너 힙에 할당되고 마이너 힙이 넘치는 순간 마이너 컬렉션이 수행되면서 살아남은 애들이 메이저 힙으로 프로모션 되는 방식이다. 마이너 힙은 Bump Pointer 방식으로 할당되기 때문에 빠르다. 그래서 마이너 힙이 클수록 작은 문제에서는 잘 동작할지도 모른다. 하지만 마이너 힙에서 살아남은 블록들이 메이저 힙으로 프로모션 될 때에는 이 블록들을 모두 복사하기 때문에 성능이 튈 수도 있다.

메이저 힙

복잡하거나 큰 데이터들은 대부분 처음부터 메이저 힙에 올라간다. 메이저 힙 컬렉션은 (1) 마킹 (2) 스윕 (3) 압축 세 페이즈가 있고, 성능을 위해서 각각을 조금씩 잘라서(slice) 동작하기 때문에 메모리 사용량이 항상 실제보다 조금 더 많을 수 밖에 없다. 문제에서 예상되는 입력이 커서 메이저 힙을 사용할 수 밖에 없는 경우 아예 처음부터 메이저 힙 크기를 크게 잡아서 메이저 컬렉션을 수행하지 않는 방향으로 하는 것이 빠를지도 모른다.

메모리 할당 방식

메모리 할당 방식은 세 가지가 있다. (1) Best Fit, (2) Next Fit, (3) First Fit.

Best Fit

두 가지 전략을 합친 할당 방식이다. 먼저, 작은 리스트나 튜플의 원소처럼, 대부분의 메이저 힙 할당이 작다는 관찰로부터 크기 별로 분류한 프리 리스트를 기반의 전략이 있다. 최대 16 워드 크기의 사이즈까지의 프리 리스트를 따로 구분해뒀다가 대부분의 할당에서 빠르게 제공한다.

두 번째 전략은, 더 큰 할당에 대해서 스플레이 트리라고 알려진 특별한 데이터 구조를 이용해서 프리 리스트를 구현한다. 이러한 검색 트리는 최근 접근 패턴에 알맞은 것으로, 가장 최근에 요청된 할당 사이즈에 가장 빠르게 접근할 수 있다는 의미이다.

크기 구분 프리 리스트에서 가능한 더 큰 사이즈가 없으면 작은 할당이 일어나고, 16 워드 이상의 큰 할당은 기본적으로 메인 프리 리스트에서 일어난다. 즉, 프리 리스트는 요청된 할당 크기만큼 큰 것 중 가장 작은 블록에 대해서 쿼리된다.

Best Fit은 OCaml 5 버전의 기본 할당 방식으로 할당 비용 (CPU) 과 힙 파편화 사이에서 적절한 트레이드 오프를 보여준다.

Next Fit

Next Fit은 가장 최근 할당 요청에 사용된 프리 리스트 블록에 대한 포인터를 유지하다가, 새로운 요청이 오면 이 포인터 다음 블록부터 프리 리스트의 끝까지, 그리고 끝까지 찾은 경우 다시 프리 리스트의 처음부터 그 블록 전까지 검색하는 전략이다.

보면 알겠지만 이 방법은 꽤 싼 할당 메커니즘인데, 같은 힙 청크를 다 쓸 때까지 할당 요청에 걸쳐 재사용할 수 있기 때문이다. 다시 말하면 CPU 캐시를 더 잘 사용하게 되어서 메모리 로컬리티가 좋다는 의미이다. 반면 가장 큰 단점은, 대부분의 할당이 작기 때문에, 프리 리스트의 시작 부분에 있는 커다란 블록이 심하게 파편화 된다는 것이다.

OCaml 4.11 버전의 기본 할당 방식으로, Best Fit은 이때 상대적으로 새롭게 추가된 전략이라서 아직 테스트가 덜 된 상황이었다.

First Fit

만약 프로그램이 아주 다양한 크기의 값을 할당하는 경우, 프리 리스트가 파편화될 수 있다. 어떤 할당 요청에 대해서 남아 있는 메모리 청크 중 아무것도 충분히 크지 못한 경우, GC는 프리 리스트에 여유 청크가 있는데도 불구하고 아주 비싼 압축을 강제로 수행해야 한다.

First Fit 할당 전략은 메모리 파편화를 줄이는데 (= 압축 횟수를 줄이는데) 초점을 맞춘 전략으로, 대신 메모리 할당 속도를 희생한다. 모든 할당은 프리 리스트를 처음부터 끝까지 스캔하면서 적절한 크기의 여유 청크를 찾는다.

부하가 있는 몇몇 리얼 타임 작업의 경우, 잦은 힙 압축을 줄이는 게 추가적인 할당을 희생하더라도 훨씬 더 좋을 수 있다.

요약

요약하면 다음과 같다.

Best Fit: OCaml 5 버전의 디폴트 할당 방식. 작은 크기의 값에 대해서는 잘 동작할테고, 크기가 크면 좀 오버헤드가 있지만 적절한 성능이다.
Next Fit: OCaml 4 버전의 디폴트 할당 방식. 가장 빠른 방식. 단 다양한 크기의 값에 대해서는 파편화가 심해져서 힙 압축이 자주 발생할 수 있기 때문에, 문제의 메모리 제한에 따라 힙 압축을 꺼버리는 것도 하나의 방법일 수 있다.
First Fit: 문제 풀이에서는 쓸 일이 없는 방식이니 잊도록 하자.

결론은, 잘 모르겠으면 그냥 디폴트 할당 방식인 Best Fit을 쓰면 되고, 문제에 따라서는 Next Fit에 추가적인 GC 튜닝을 하면 효과를 볼 수 있을지도 모른다.

Gc 모듈

Gc 모듈을 이용하면 Gc를 들여다보거나 조절하는 것이 가능하다. 먼저 현재 Gc 상태를 나타내는 stat 타입이 있다. Gc를 튜닝하고 싶다면 먼저 Gc.stat ()을 호출해서 Gc 상태를 확인한 후에 파라미터를 튜닝하도록 하자.

type stat = {
  minor_words: float;  (* 프로그램 시작 후부터 마이너 힙에 할당된 워드의 수 *)
  promoted_words: float;  (* 프로그램 시작 후부터 마이너 힙에 할당되어 마이너 컬렉션에서 살아남아서 메이저 힙으로 옮겨간 워드의 수 *)
  major_words: float;  (* 프로그램 시작 후부터 메이저 힙에 할당된 수로, 프로모트된 마이너 힙의 워드까지도 포함한다. *)
  minor_collections: int;  (* 프로그램 시작 이래 마이너 컬렉션 횟수 *)
  major_collections: int;  (* 프로그램 시작 이래 메이저 컬렉션 사이클 완료 횟수 *)
  heap_words: int;  (* 메이저 힙의 전체 크기 (워드) *)
  heap_chunks: int;  (* 메이저 힙을 구성하는 연속된 메모리 조각의 개수 *)
  live_words: int;  (* 메이저 힙에 살아있는 데이터의 워드 수 *)
  live_blocks: int;  (* 메이저 힙에 살아있는 블록 수 *)
  free_words: int;  (* 프리 리스트에 있는 워드 수 *)
  free_blocks: int;  (* 프리 리스트에 있는 블록 수 *)
  largest_free: int;  (* 프리 리스트에 있는 가장 큰 블록의 크기 (워드) *)
  fragments: int;  (* 단편화로 인해서 낭비되는 워드의 수. 할당에 쓸 수 없는 것으로, 두 개의 살아있는 블록 사이에 있는 1 워드 짜리 프리 블록들의 개수이다. *)
  compactions: int;  (* 프로그램 시작 이후 힙 압축 횟수 *)
  top_heap_words: int;  (* 메이저 힙에서 도달 가능한 최대 사이즈 (워드) *)
  stack_size: int;  (* 현재 스택 크기 (워드) *)
}

그리고 Gc에 쓰이는 다양한 파라미터들을 튜닝하기 위한 control 타입이 있다.

type control = {
  mutable minor_heap_size: int;
  mutable major_heap_increment: int;
  mutable space_overhead: int;
  mutable verbose: int;
  mutable max_overhead: int;
  mutable stack_limit: int;
  mutable allocation_policy: int;

  window_size: int;
  custom_major_ratio: int;
  custom_minor_ratio: int;
  custom_minor_max_size: int;
}

현재 control 설정 값은 Gc.get ()을 호출해서 알아낼 수 있다. 이 값을 튜닝하려면 Gc.set { (Gc.get ()) with Gc.verbose = 0x00d }와 같이 호출할 수 있다. 이 중에서 우리가 관심을 갖고 지켜봐야 할 값은 다음과 같다.

`control`	설명
`minor_heap_size`	마이너 힙의 크기 (워드) 를 설정한다. 이 값을 바꾸면 곧바로 마이너 컬렉션이 수행된다. 디폴트는 256k.
`major_heap_increment`	메이저 힙을 늘릴 때 추가할 힙의 크기. 이 값이 1,000 이하인 경우 백분율 의미하고 (즉 100으로 설정하면 100% 증가 = 두 배 증가이다), 1,000보다 크면 힙에 추가되는 고정 워드 수를 의미한다. 디폴트는 15 (즉, 15%)
`space_overhead`	메이저 GC 속도는 이 파라미터로부터 계산된다. 이 값은 GC가 당장 unreachable 블록을 수집하지 않아서 "낭비"되는 메모리이다. 살아있는 데이터에 사용되는 메모리에 대한 백분율로 표시된다. 이 값이 작으면, 즉 수집하지 않을 블록이 더 적으면, GC가 더 많이 작동하고, 따라서 더 많은 CPU 시간을 사용하여 더 열심히 블록을 수집한다. 기본 값은 120이다.
`verbose`	GC 관련 메시지를 표준 에러로 출력하는 것을 조절한다. 몇 가지 값의 합으로 조절 가능하다. `0x001`: 메이저 GC 싸이클의 시작과 끝 `0x002`: 마이너 컬렉션과 메이저 GC 슬라이스 `0x004`: 힙의 성장과 줄어듦 `0x008`: 스택과 메모리 매니저 테이블의 크기 변경 `0x010`: 힙 압축 `0x020`: GC 파라미터 변경 `0x040`: 메이저 GC 슬라이스 크기 계산 `0x080`: finalisation 함수 호출 `0x100`: 프로그램 시작 시에 바이트코드 실행 파일과 공유 라이브러리 탐색 `0x200`: 힙 압축을 수행하는 조건에 대한 계산 `0x400`: 프로그램 종료 시 GC 통계를 출력 기본 값은 0이다.
`max_overhead`	"낭비"되는 메모리의 예상 크기가 살아있는 데이터의 `max_overhead` 백분율보다 크면 힙 압축이 수행된다. 이 값이 0이면 메이저 GC 싸이클의 끝마다 힙 압축이 수행된다 (테스트 용도). 이 값이 1,000,000 보다 크면 압축을 수행하지 않는다. 만약 압축을 완전히 끌 거라면 할당 전략을 Best Fit으로 하는 것을 강하게 추천한다. 디폴트 값은 500.
`allocation_policy`	0: Next Fit 1: First Fit 2: Best Fit 디폴트는 0(Next Fit)이다.
`window_size`	메이저 GC가 워크로드의 변화를 완화하기 위해서 사용하는 윈도우 크기. 1~50 사이 정수 값을 갖는다. 디폴트 값은 1.

보면 알겠지만 마이너 힙을 조절할 수 있는 파라미터는 minor_heap_size 하나 뿐이고 나머지는 대부분 메이저 힙에 대한 파라미터이다. 그 외에 커스텀 할당과 관련된 파라미터도 있는데 이것은 문제 풀이의 범위를 벗어나기 때문에 여기서는 제외했다.

문제 풀이에서는 (1) 최대한 마이너 힙만을 쓰거나, (2) 메이저 컬렉션을 최대한 미루거나, 아니면 (3) 메이저 힙을 쓰되 파편화 신경쓰지 않고 할당 속도를 높이는게 중요하다. 따라서 가능한 세 가지 접근이 있다.

마이너 힙 늘리기

문제의 모든 할당이 충분히 작아서 마이너 힙을 키우면 될 것 같은 경우, 다음과 같이 세팅해볼 수 있다.

let () = Gc.set { (Gc.get ()) with Gc.minor_heap_size = 1_280_000 }

메이저 컬렉션 미루기

사실 메이저 힙에 메모리를 아예 할당하지 않는 것은 꽤 어렵다. 그것보다는, 어차피 문제 풀이에서는 테스트 셋만 통과하면 되니까, 메이저 힙 컬렉션을 아예 하지 않으면 추가적인 오버헤드가 없을 것이다. 하지만 이것은 더 예측하기 어려운데, 왜냐하면 메이저 힙 컬렉션을 안해버리면 거의 반드시 메모리 제한을 초과해버리기 때문이다.

따라서 가장 적당한 접근은 메이저 컬렉션을 최대한 미루는 것이다. 문제는 이것 역시 손쉽게 판단하기 어렵다는 것이다. 문제와 문제의 테스트 셋 특성에 따라서 메이저 힙의 공간 오버헤드를 얼마나 크게 가져갈 수 있을지가 다르다. 기본 값은 120 (살아있는 데이터의 120%) 인데, 문제마다 다양하게 실험해보고 적당한 값을 찾아야 한다.

let () = Gc.set { (Gc.get ()) with Gc.space_overhead = 1000 }

힙 압축 안하기

백준 채점용 컴파일러인 4.11.1에서는 이미 디폴트 할당 방식이 0 (Next Fit)이므로 할당 속도에는 문제가 없다. 힙 압축을 아예 꺼버리면 혹시나 발생할지 모를 힙 압축을 아예 하지 않을 수 있다.

let () = Gc.set { (Gc.get ()) with Gc.max_overhead = 1_000_001 }

예시

백준 11725번을 해시 테이블 + 정수 셋을 이용한 그래프로 풀면 3회 평균 297ms의 시간과 46MB 메모리가 나온다. 여기에 위의 Gc 정책을 각각 적용해보면 다음과 같다.

마이너 힙 늘리기: 286ms / 59MB
메이저 컬렉션 미루기 (1000%): 221ms / 49MB
메이저 컬렉션 미루기 (2000%): 204ms / 55MB
메이저 컬렉션 미루기 (2500%): 208ms / 53MB
메이저 컬렉션 미루기 (3000%): 233ms / 52MB
힙 압축 안하기: 309ms / 46MB
셋 다 적용: 250ms / 66MB

문제의 성격에 따라 당연히 다르겠지만 이 문제에서는 메이저 컬렉션만 미뤘을 때 (오버헤드 2000%) 가장 평균적인 속도가 빨랐다. 혹시 몰라서 마이너 힙 크기를 두 배 늘렸더니 메모리 사용량은 20MB 정도 늘어났지만 속도는 오히려 떨어졌기 때문에, 마이너 힙이 크다고 항상 좋은 것은 아닌 것 같다. 그리고 메이저 컬렉션을 미루기 위한 공간 오버헤드가 3000%을 넘어가니 유의미한 효과가 없었고, 10,000% 이상으로 주니 메모리 초과가 발생했다.

사실 정확한 측정을 하려면 수행 횟수를 최소 30번은 해야겠지만 그러긴 힘들어서 여기서는 3번의 수행만을 했기 때문에 오차 범위가 꽤 크다는 염두에 점을 두자. 그럼에도 불구하고 Gc를 튜닝하는 것이 문제 풀이 속도에 영향을 주는 것을 눈으로 확인할 수 있었기 때문에 문제에 맞게 이를 잘 활용하면 좋겠다. 그리고 무엇보다 문제와 채점 데이터의 성격에 따라서 작은 튜닝이 큰 영향을 줄 수 있기 때문에, 모든 문제에 맞는 은 총알은 없다는 것을 반드시 기억해야 한다.

Functional Approaches

"함수형"에 대한 명확하고 합의된 정의가 있는 것은 아니지만, imperative 언어나 객체 지향 언어와는 확실히 다른 패러다임이 존재하는 것은 확실하다. 그리고 많은 경우 이러한 함수형 접근의 특징 덕분에 함수형으로 작성한 코드는 imperative counterparts에 비해서 훨씬 더 밀도가 깊다(dense). 그래서 코드 한 줄이 하는 일이 생각보다 많아지지만, 대신 그 빽빽한 한 줄이 무엇을 하는지 확실하게 추상화해놓고 더 중요한 문제에 집중할 수 있다.

Pipelining

OCaml 표준 라이브러리에는 다음과 같이 정의된 파이프라이닝 중위 연산자가 있다.

val ( |> ) : 'a -> ('a -> 'b) -> 'b

이게 왜 유용할까? 우리가 문제를 풀기 위해서 문제를 잘개 쪼개어 풀 때, f를 먼저 생각하기 보다는 x를 먼저 생각하는 것이 더 자연스럽기 때문이다. 예를 들어 백준 1269번 문제를 보자. 이 문제의 입력은 (n, m을 제외하면) 공백으로 구분된 정수를 담은 한 줄로 된 문자열이다. 그렇다면 문제를 풀기 위해서 이 문자열을 원하는 입력으로 처리하는 자연스러운 과정을 생각해보면 다음과 같다.

문자열 한 줄을 입력 받아서 저장한다.
저장한 문자열을 공백을 기준으로 쪼개어 문자열의 리스트를 만든다.
문자열의 리스트를 정수 리스트로 변환한다.
정수 리스트의 모든 원소를 정수 집합에 추가한다.

이걸 파이프라이닝을 쓰지 않고 처리하면 다음과 같다.

let s = read_line () in
let xs = String.split_on_char ' ' s in
let is = List.map int_of_string xs in
let set = List.fold_left (fun acc x -> IntSet.add x acc) IntSet.empty is in
set

한 줄 한 줄 따라 읽으면 잘 이해는 되지만, 결국 최종적으로 set이라는 하나의 데이터를 만들어 내는 코드이므로 이를 위해 s, xs, is 등의 중간 변수들은 사실 불필요한 인지적 부하를 일으킨다. 그래서 이 작업을 한 줄로 처리하려면 다음과 같이 해야한다.

let set = List.fold_left (fun acc x -> IntSet.add x acc) IntSet.empty (List.map int_of_string (String.split_on_char ' ' (read_line ()))) in
set

이렇게하면 중간 변수들이 사라지긴 하지만, 대체 무슨 작업을 하는 코드인지 한눈에 파악하기가 굉장히 어려워진다. 그 이유는 f (f (f ... (f x)))와 같이, 바깥의 f에 적용하기 위한 파라미터를 계산하려면 안쪽의 (f ... (f x))를 평가해야 하기 때문이다. 즉, 다음과 같이 코드를 읽는 순서가 거꾸로다:

정수 리스트의 모든 원소를 정수 집합에 추가할 건데, 그 정수 리스트는;
문자열의 리스트를 변환한 것이고, 이 문자열의 리스트는;
어떤 문자열을 공백을 기준으로 쪼개어 문자열의 리스트로 만든 것이고, 이 문자열은;
입력으로 받은 문자열 한 줄이다.

파이프라이닝은 이러한 경우에 오컴의 면도날처럼 훌륭한 해결책을 제시한다: 중간 변수도 필요하지 않으며, 생각의 순서가 자연스럽다.

let set =
  read_line ()
  |> String.split_on_char ' '
  |> List.map int_of_string
  |> List.fold_left (fun acc x -> IntSet.add x acc) IntSet.empty
in
set

사실 많은 OCaml 함수들이 이런 파이프라이닝 (을 포함한 많은 체이닝 연산들) 을 염두에 두고, 가장 중요한 파라미터를 마지막에 받고 있다. 즉, String.split_on_char의 타입은 char -> string -> string으로 string을 가장 나중에 받고 있고, List.map 역시 ('a -> 'b) -> 'a list -> 'b list로 'a list를 마지막에 받는다. 그 덕분에 이러한 자연스러운 파이프라이닝이 가능한 것이다.

Map, Filter, Fold

Currying

Functor

Option

Monad

모나드를 뭐 카테고리 이론에서 빌려온 유서 깊은 어쩌구 저쩌구.... 이렇게 접근하면 겁먹고 이해하는데 실패한다.

모나드는 별게 아니라 디자인 패턴으로 접근하면 사용하기 좋다. 예를 들어, 패턴 매칭을 할 때 디폴트 패턴에 대해서 trivial한 작업만이 필요하고, 진짜 관심있는 데이터에 대해서는 많은 작업이 필요할 때, 모나드를 적용하면 코드가 깔끔해진다.

match foo y with
| Default -> ()
| Complex x -> ... very long long work for x ...

위와 같은 코드가 있을 때, bind를 아래와 같이 정의하고

let bind x f = match x with
  | Default -> ()
  | Complex x -> f x

중위 연산자 >>=, 또는 Let Syntax let*을 아래와 같이 정의하면

let ( >>= ) = bind

let ( let* ) = bind

원래 코드를 아래와 같이 깔끔하고 읽기 쉽게 만들어주는 문법 또는 디자인패턴이 바로 모나드라고 생각하면 된다.

foo y >>= fun x -> ... very long long work for x ...

(* or *)

let* x = foo y in
... very long long work for x ...

Option Monad

가장 쉽고 직관 적인 예시로, Option 모듈에 있는 bind가 있다.

let bind o f = match o with None -> None | Some v -> f v

역시 이 bind를 >>= 또는 let* 으로 재정의해서 쓸 수 있다.

bind의 타입을 보면 좀더 이해하기 쉽다.

val bind : 'a option -> ('a -> 'b option) -> 'b option

즉 다음 두 가지 조건이 갖춰졌을 때, bind 모나드를 활용한다면 훨씬 코드를 읽기 수월해질 것이다. 어떤 옵션 값에 대해서,

옵션이 None 일 때에는 아주 trivial한 작업, 여기서는 그냥 그대로 None을 흘려 보내는 일만이 필요하다.
옵션의 실제 값 Some v에 대해서는, 안쪽 값 v를 가지고 이것저것 작업을 하고 최종적으로 어떤 옵션 값을 만들어내면 된다.

이런 경우에 모나드 문법을 적용하면, trivial한 작업에 대해서 실수할 일도 적어지고, 또 진짜 집중해야 하는 값에 대한 작업을 하는 코드도 읽기 수월해진다.

Some Data Structures

Tree

Disjoint Set

Priority Queue

Basic Algorithms

기본적인 알고리즘을 살펴보자.

Bisect

이분 탐색을 일반화해서 정렬된 배열 arr과 찾고자 하는 값 x가 있을 때, x가 속한 범위의 Lower Bound와 Upper Bound 를 구할 수 있다. C++에서는 std::lower_bound 와 std::upper_bound 함수가 제공되고 Python에서는 bisect_left와 bisect_right가 제공된다.

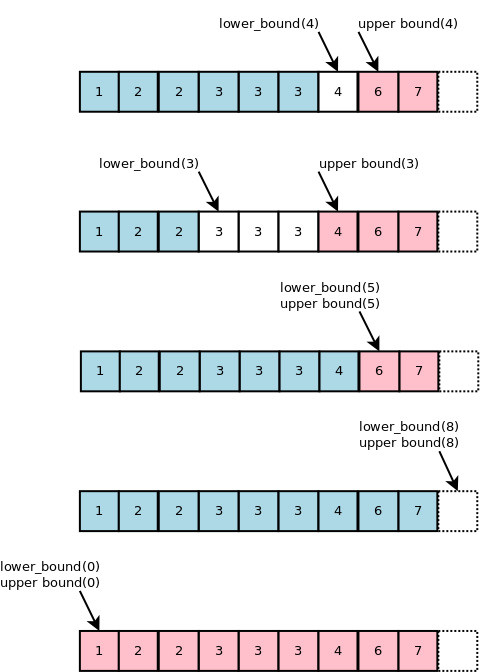
c++ bisect

위의 그림에서 볼 수 있는 것처럼 bisect에는 두 가지 특징이 있다.

x가 존재한다면, Lower Bound는 그 시작점의 인덱스이고 Upper Bound는 끝나는 지점의 다음 인덱스 이다. 즉, [lower_bound, upper_bound)의 Half-open range로 표현된다.
x가 없는 경우 lower_bound == upper_bound가 된다. Half-open range에서 공집합과 같은 의미이다.

보통 Lower Bound나 Upper Bound 하나만 찾으면 되는 문제가 많다. x 값의 인덱스를 포함할 수도 있는 Lower Bound를 자주 쓰기에 이를 좀더 살펴보자.

Lower Bound 값이 배열 범위를 벗어나면 찾으려는 x값이 없다는 의미이다. 이는 자명하다.
Lower Bound 값이 배열 범위 내 [0, len)에 있더라도, 직접 해당 인덱스의 값이 x와 같은지 한번 더 확인해야 한다. 그 이유는 만약 찾으려는 값이 없으면서 배열의 모든 값보다 작을 때 Lower Bound의 값이 0이기 때문이다.

이를 바탕으로 OCaml의 bisect를 구현하면 다음과 같다.

let bisect ?(left = true) arr x =
  let low, high = 0, Array.length arr in
  let rec loop low high =
    if low >= high then low
    else (
      let mid = (low + high) / 2 in
      if left then (
        if x <= arr.(mid) then loop low mid else loop (mid + 1) high
      ) else (
        if x < arr.(mid) then loop low mid else loop (mid + 1) high
      )
    )
  in
  loop low high

OCaml Problem Solving